Уравнения Навье-Стокса в декартовых координатах

Уравнения движения вязкой жидкости можно получить путем прибавления выражения 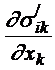 к правой части уравнений Эйлера

.

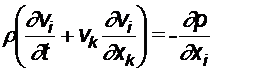Получаем,

.

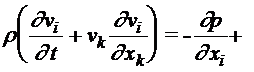
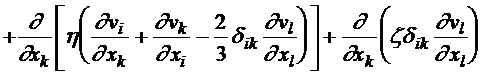Величины h и z являются в общем случае функциями давления и температуры. Поэтому они не постоянные в объеме и не могут быть вынесены из-под знака производной.

При постоянных значениях коэффициентов вязкости уравнения Навье-Стокса в векторной форме имеют вид

.

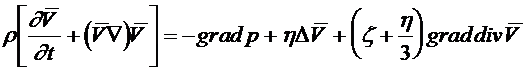Уравнения были впервые сформулированы Навье в 1827 году, вывод уравнений близкий к современному, был дан Стоксом в 1845 году.

Если жидкость считать несжимаемой, то   и последний член исчезает

.

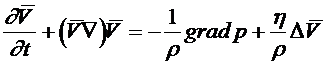Тензор напряжений в несжимаемой жидкости принимает более простой вид

.

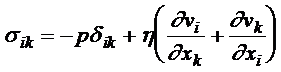Отношение  называют кинематической вязкостью, h - динамической вязкостью.

Граничные условия

Между поверхностью твердого тела и вязкой жидкостью существуют силы межмолекулярного сцепления, приводящие к тому, что прилегающие к твердой стенке слой жидкостью как бы прилипает к ней.

Граничные условия к уравнениям движения вязкой жидкости состоит в требовании обращения в нуль скорости жидкости на неподвижных твердых поверхностях .

В общем случае движущейся поверхности скорость   должна быть равна скорости этой поверхности.