Течение по трубе

Известно несколько точных решений для уравнений Навье-Стокса. Рассмотрим одно из них - для случая стационарного течения жидкости в трубе произвольного сечения ( одинакового вдоль всей длины трубы ).

Ось трубы выберем в качестве оси  . Очевидно, что скорость  жидкости направлена везде по оси  и является функцией только от  и .

Уравнение неразрывности удовлетворяется тождественно, а проекции на оси  и  из системы уравнений Навье-Стокса дают

.

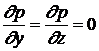То есть давление постоянно вдоль сечения трубы. Уравнение в проекции на ось х дает

.

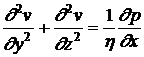Откуда имеем, что 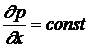, градиент давления можно записать в виде  , где   - разность давлений на концах трубы, а   - ее длина.

Распределение скоростей в потоке жидкости в трубе определяется двумерным уравнением типа

.

Уравнение должно быть решено при граничном условии  на контуре сечения трубы.

Решим это уравнение для трубы кругового сечения. Выбирая начало координат в центре трубы кругового сечения и вводя полярные координаты, имеем в силу симметрии  .

Воспользуемся выражением для оператора Лапласа в полярных координатах, имеем

.

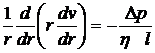Интегрируя, находим

.

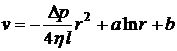Постоянную  a  надо положить равной нулю, поскольку скорость должна оставаться конечной во всем сечении трубы, включая ее центр.

Постоянную  b  определим из требования  , при r = R ( где R - радиус трубы ) и получаем

.

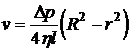Таким образом, скорость распределена по сечению трубы по параболическому закону.

Определим расход жидкости в трубе - количество ( массу ) жидкости  Q, протекающей в 1 секунду, через поперечное сечение трубы.

Через кольцевой элемент  площади сечения трубы проходит в 1 секунду количество жидкости .

Поэтому

.

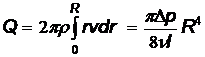Количество протекающей жидкости пропорционально четвертой степени радиуса трубы.