Изучение движения газов с высокими скоростями, достигающими скорости звука, является предметом газовой динамики. Одной из фундаментальных задач последней является исследование течений без учёта сопротивлений и в отсутствие теплообмена (т.е.) адиабатических. В этих условиях уравнение баланса удельной энергии имеет вид
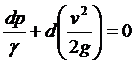 .
.
Уравнение адиабаты идеального газа представим в виде
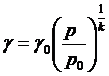 .
.
Будем отмечать в дальнейшем индексом "0" величины, характеризующие газ, находящийся в покое, или, как говорят в газодинамике, в заторможенном состоянии, подставим в уравнение неразрывности
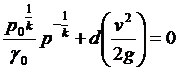
и после интегрирования
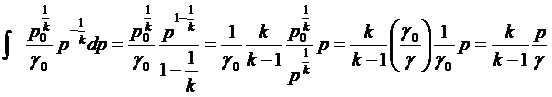 .
.
При установившемся течении весовой расход газа во всех сечениях по длине газопровода одинаков в течение всего процесса движения.
Следовательно, при установившемся течении
![]() ,
,
что является выражением условия неразрывности при движении газа (и также сжимаемых жидкостей). В трубопроводе постоянного сечения одинаковой по длине трубопровода будет также весовая скорость
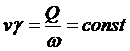 .
.
Изменение в удельном весе (плотности) идеального газа при изменении давления и температуры выражаются законом Клайперона-Менделеева
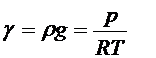 ,
,
где Т - абсолютная температура газа, R - газовая постоянная.
В технике имеют особое значение изотермическое и адиабатическое течения газа. При изотермическом (Т=const) течении идеального газа зависимость между давлением и плотностью имеет вид
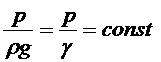 ,
,
при адиабатическом
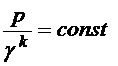 ,
,
где 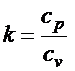 - показатель адиабаты, cp - удельная теплоёмкость газа при постоянном давлении, cv - удельная теплоёмкость газа при постоянном объёме.
- показатель адиабаты, cp - удельная теплоёмкость газа при постоянном давлении, cv - удельная теплоёмкость газа при постоянном объёме.
Имея в виду последнее соотношение, можно записать
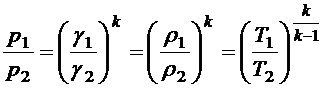 ,
,
получаем
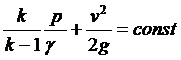 .
.
Имея в виду, что v = 0 при p=p0 (состояние покоя), найдём:
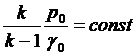 ,
,
или
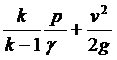
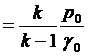 .
.
Поможем написать любую работу на аналогичную тему

