Запишем уравнение Бернулли в дифференциальной форме
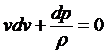 .
.
Преобразуем уравнение Бернулли для газа так, чтобы можно было ввести число Маха. Имеем
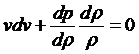 ,
,
квадрат скорости звука 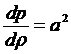 , тогда
, тогда
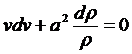 .
.
Поделим на a2, получим
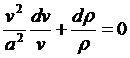 ,
,
или в окончательном виде
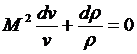 ,
,
где M - число Маха.
Другим уравнением, необходимым для анализа течений газа в трубе переменного сечения, является уравнение неразрывности, или сохранения массы.
Будем рассматривать одномерное установившееся течение газа вдоль трубы переменного сечения, при этом предположим, что параметры потока газа, такие, как скорость потока, давление и плотность, одинаковы во всех точках каждого из конечных сечений, перпендикулярных к оси трубы.
Это предположение довольно хорошо соответствует действительности для элементарной трубки тока, но его применяют и для труб конечных размеров, используя средние величины по сечениям трубы.
Через каждое поперечное сечение трубы в случае одномерного течения проходит за 1 с масса газа m=Svr, где S - площадь поперечного сечения трубы, v - скорость течения газа, r - плотность газа. При установившемся течении через все поперечные сечения должна пройти одна и та же масса газа, т.е.
![]() .
.
Прологарифмируем это уравнение сохранения массы. Получим
![]() .
.
Считая переменными величины S, v, r, возьмём полные дифференциалы от обеих частей. Имеем
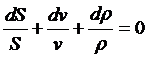 .
.
Это и есть уравнение неразрывности для установившегося одномерного течения идеального газа в трубе переменного сечения.
|
|
Из уравнения неразрывности и уравнения Бернулли исключим величину
Это уравнение носит название уравнения Гюгонио. Используя уравнение Гюгонио, проанализируем характер возможных течений газа в трубе переменного сечения. |
Из уравнений следует:
1) при M<1, что соответствует дозвуковым течениям, знаки величин dS и dv противоположны, т.е. там, где возрастает S, в направлении течения скорость должна убывать, и наоборот,
2) для сверхзвуковых течений M>1, знаки dS и dv одинаковы, т.е. сверхзвуковой поток расширяется противоположно дозвуковому. Чтобы увеличить его скорость, трубу следуeт расширить,
3) при M = 1 имеем dS = 0, т.е. в этом случае S достигает максимума или минимума. Можно показать, что M = 1 может быть только в самом узком сечении трубы, где S=Smin.
Выводы о характере течений газа в трубах переменного сечения нашли применение в конструкциях сопел современных ракетных двигателей и аэродинамических трубах больших скоростей. Для получения больших сверхзвуковых скоростей выходящего из сопла газа следует сначала сопло сужать, чтобы получить звуковую скорость газа в узком сечении сопла, а затем сопло надо расширять для дальнейшего увеличения скорости выходящего из него газа.
|
|
Наибольшая скорость, которая может быть получена на выходе из сопла, зависит от площади выходного сечения и должна обеспечиваться необходимым для данной скорости давлением на входе в сопло ( рис. 58 ).
|
Поможем написать любую работу на аналогичную тему


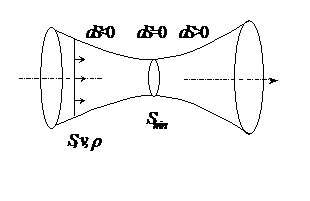 Рис. 57
Рис. 57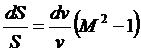 .
.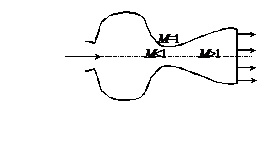 Рис. 58
Рис. 58