Параметры газа, соответствующие нулевой скорости потока, называются параметрами торможения. Давление, плотность, температура и энтальпия, соответствующие этому состоянию называются давлением, плотностью, температурой и энтальпией торможения и обозначаются po, ro, To, io. Соотношение между местными параметрами потока и параметрами торможения определяются с помощью газодинамических функций t, p, e.
Аргументом газодинамических функций является число Маха
![]() или коэффициент скорости
или коэффициент скорости 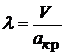 . Где V - местная скорость потока, а - скорость звука в газе,
. Где V - местная скорость потока, а - скорость звука в газе, ![]() - критическая скорость звука. Установим связь между числом Маха и коэффициентом скорости. Запишем уравнение энергии в виде
- критическая скорость звука. Установим связь между числом Маха и коэффициентом скорости. Запишем уравнение энергии в виде
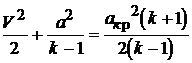 .
.
Разделим уравнение на ![]() , получим
, получим
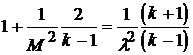 .
.
Отсюда
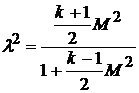
или разрешив относительно числа Маха, имеем
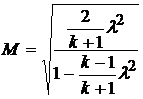 .
.
Для вывода газодинамических функций запишем уравнение энергии
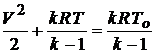 .
.
Умножим уравнение на ![]() и учтем, что
и учтем, что ![]() . В результате имеем
. В результате имеем
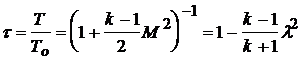 .
.
Уравнение состояния газа ![]() , записанное для параметров торможения
, записанное для параметров торможения ![]() , позволяет получить соотношение
, позволяет получить соотношение
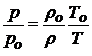 .
.
Из уравнения адиабаты 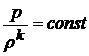 по аналогии для параметров торможения имеем
по аналогии для параметров торможения имеем
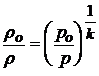 .
.
Из последних трех равенств имеем
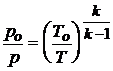 ,
, 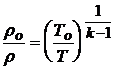 .
.
Воспользуемся теперь выражением для газодинамической функции t, запишем
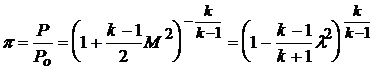 ,
,
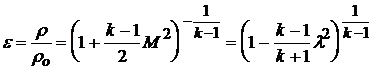 .
.
Газодинамические функции широко используются для расчета изэнтропических течений газа. Во многих учебниках по газовой динамике они представлены в виде таблиц. Из выражений для газодинамических функций при М = l = 1 критические параметры газа могут быть найдены через параметры торможения po, ro, To
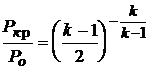 ,
, 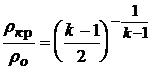 ,
, 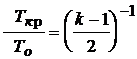 .
.
При практических расчетах используют еще одну газодинамическую функцию, называемую удельным секундным расходом q :
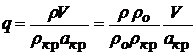 .
.
Воспользовавшись выражением для газодинамической функции e а также связью между критическими параметрами и параметрами торможению, учитывая 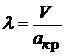 , имеем
, имеем
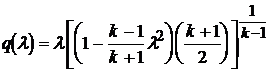 .
.
Нетрудно заметить, что при l = 0 и ![]() получим q=0. В первом случае расход равен нулю, так как газ неподвижен. Во втором случае p = r = T = 0.
получим q=0. В первом случае расход равен нулю, так как газ неподвижен. Во втором случае p = r = T = 0.
Поможем написать любую работу на аналогичную тему

