Одним из существенных свойств сверхзвукового потока является возможность существования ударных волн. Ударная волна или скачок уплотнения - это область сверхзвукового течения, в которой происходит резкое уменьшение его скорости и рост давления, температуры плотности и энтропии. Толщина ударной волны мала - порядка средней длины свободного пробега молекул. При решении многих задач газовой динамики толщиной ударной волны пренебрегают.
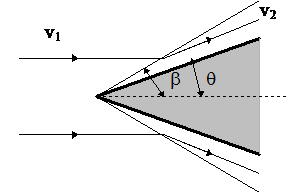
Ударная волна, скачок уплотнения, распространяющаяся со сверхзвуковой скоростью тонкая переходная область, в которой происходит резкое увеличение плотности, давления и скорости газа. Ударные волны возникают при взрывах, при сверхзвуковых движениях тел. Ударная волна, в которой вектор скорости набегающего потока направлен по нормали к поверхности разрыва параметров, называется прямым скачком уплотнения. В прямом скачке уплотнения линия тока не изменяет своего направления, поэтому течение можно считать одномерным. Косым скачком называется такое течение, вектор скорости направлен под острым углом к фронту ударной волны. При косом скачке уплотнения происходит поворот вектора скорости на некоторый угол q. Плоскость разрыва параметров ( скачка ) располагается по отношению к вектору скорости набегающего потока под углом b. При обтекании сверхзвуковым потоком клина ( рис. 63 ) течение вдоль боковой поверхности клина отделяется от набегающего потока плоским скачком уплотнения, идущим от вершины клина. При углах раскрытия клина, больших некоторого предельного, скачок уплотнения становится криволинейным, отходит от вершины клина и за ним появляется область с дозвуковой скоростью течения газа. Такая картина течения характерна для сверхзвукового обтекания тел с тупой головной частью ( рис. 64 ).
|
Рис. 63 |
Рис. 64 |
Классическим примером возникновения и распространения ударных волн в газе - это сжатие газа в трубе поршнем. Если поршень вдвигается в газ медленно, то по газу со скоростью звука распространяется, акустическая ( упругая ) волна сжатия. Если скорость поршня соизмерима со скоростью звука, возникает ударная волна. Скорость распространения ударной волны по невозмущенному газу больше скорости движения частиц газа, которая совпадает со скоростью поршня.
При теоретических исследованиях толщиной ударной волны пренебрегают, фронт ударной волны заменяют поверхностью разрыва, считают, что при прохождении через ударную волну параметры газа изменяются скачком.
Значения параметров газа по обе стороны скачка связаны соотношениями, вытекающими из законов сохранения массы, импульса и энергии :
![]()
![]()
![]()
где ![]() - соответственно давление, плотность и удельная внутренняя энергия газа, индексом 1 отмечены параметры до ударной волны, 2 - за ударной волной.
- соответственно давление, плотность и удельная внутренняя энергия газа, индексом 1 отмечены параметры до ударной волны, 2 - за ударной волной.
Исключая из равенств скорости, можно получить уравнение ударной адиабаты
![]()
![]()
где ![]() - удельный объем,
- удельный объем, ![]() - удельная энтальпия.
- удельная энтальпия.
Если известны термодинамические свойства вещества, т.е. функция ![]() или
или ![]() , то ударная адиабата дает зависимость конечного давления
, то ударная адиабата дает зависимость конечного давления ![]() от конечного объема
от конечного объема ![]() при ударном сжатии газа из начального состояния
при ударном сжатии газа из начального состояния ![]() , т.е. зависимость
, т.е. зависимость
![]() .
.
При переходе через ударную волну энтропия вещества s меняется, причем скачок энтропии ![]() для данного вещества определяется только законами сохранения, которые допускают существование двух режимов : скачка сжатия ( r2
> r1
, p2 > p1) и скачка разрежения ( r2 < r1 , p2 < p1). Однако в соответствии со вторым началом термодинамики реально осуществляется только тот режим, при котором энтропия возрастает. В обычных веществах энтропия возрастает только в ударных волнах сжатия, поэтому ударная волна разрежения не реализуется ( теорема Цемплена ).
для данного вещества определяется только законами сохранения, которые допускают существование двух режимов : скачка сжатия ( r2
> r1
, p2 > p1) и скачка разрежения ( r2 < r1 , p2 < p1). Однако в соответствии со вторым началом термодинамики реально осуществляется только тот режим, при котором энтропия возрастает. В обычных веществах энтропия возрастает только в ударных волнах сжатия, поэтому ударная волна разрежения не реализуется ( теорема Цемплена ).
Ударная волна распространяется по невозмущенному газу со сверхзвуковой скоростью v1 > a1 ( где а1 - скорость звука в невозмущенном газе ) тем большей, чем больше интенсивность ударной волны, т.е. чем больше (p2 - p1)/ p1. При стремлении интенсивности ударной волны к нулю скорость ее распространения стремится к а1 . Скорость ударной волны относительно сжатого газа, находящегося за ней, является дозвуковой : v2 < a2 ( где а2 - скорость звука в cжатом газе за ударной волной ).
В идеальном газе с постоянными теплоемкостями уравнение состояния имеет предельно простой вид : ![]() ,
, ![]() , где
, где ![]() - показатель адиабаты, отношение теплоемкостей при постоянных давлении и объеме, R - универсальная газовая постоянная, m - молекулярный вес. Уравнение ударной адиабаты можно получить в явном виде :
- показатель адиабаты, отношение теплоемкостей при постоянных давлении и объеме, R - универсальная газовая постоянная, m - молекулярный вес. Уравнение ударной адиабаты можно получить в явном виде :
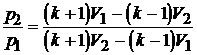 .
.
|
Рис. 65 |
Ударная адиабата, или адиабата Гюгоньо Н, отличается от обычной адиабаты Р ( адиабаты Пуассона ), для которой
На рис. 65 показаны ударная адиабата Н и адиабата Пуассона Р, проходящая через общую точку А исходного состояния. |
При ударном сжатии газа для данного изменения V необходимо большее изменение р, чем при адиабатическом сжатии. Это является следствием необратимости нагревания при ударном сжатии, связанного, в свою очередь, с переходом в тепло кинетической энергии потока, набегающего на фронт ударной волны. В силу соотношения
![]() ,
,
следующего из системы уравнений, связывающей параметры на ударной волне, скорость ударной волны определяется наклоном прямой, соединяющей точки начального и конечного состояния ( рис. 65 ).
Параметры газа на ударной волне можно связать с числом Маха M=vв/a1 :
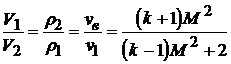 ,
,
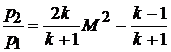 ,
,
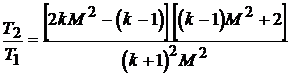 .
.
В пределе для сильных ударных волн при М®¥, 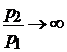 получаем :
получаем :
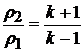 ,
, ![]()
![]()
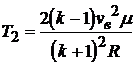 .
.
Поможем написать любую работу на аналогичную тему




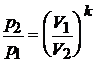 .
.