Критерии подобия

Рассмотрим условия динамического подобия при обтекании тел потоком вязкого сжимаемого газа. Для этого запишем систему уравнений - неразрывности, количества движения, энергии и состояния газа, а также соответствующие граничные и начальные условия. При этом будем считать  m = const, l = const, cp = const. Примем за характерную длину некоторый линейный размер летательного аппарата L. Другими  характерными параметрами являются характеристики невозмущенного потока :  V¥ - скорость,  r¥ - плотность, р¥ - давление, T¥ - температура,  i¥ - энтальпия.

Введем безразмерные величины :

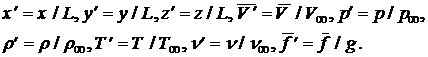
Здесь  - единичный вектор массовой силы.

Преобразуем сначала уравнение количества движения и уравнение неразрывности, выражая в них все размерные величины через безразмерные, получим

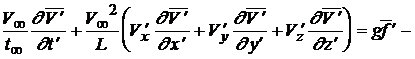
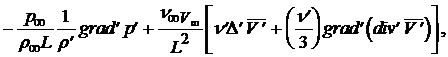
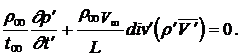
Здесь символы  означают, что дифференцирование производится в безразмерных координатах.

Уравнения являются размерными. Однако в них размерные величины представлены в виде коэффициентов с одинаковыми размерностями. В уравнениях такими размерными множителями являются

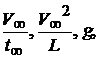
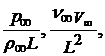
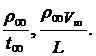
Поделив на любой из указанных размерных множителей, получим уравнения в безразмерной форме.

Для того чтобы получить критерии подобия, разделим обе части уравнения количества движения на величину . , а уравнения неразрывности - на 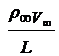 . Тогда

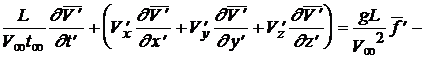
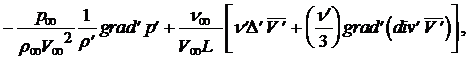
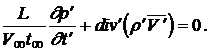
Здесь

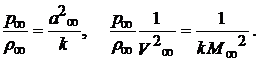
Аналогично выполняется обезразмеривание уравнения энергии. В уравнениях и граничных условиях будут содержится ряд безразмерных параметров, составленных из размерных величин :

число Фруда ,

число Рейнольдса  ,

число Эйлера ,

число Струхаля ,

число Маха М = V/a,

число Прандтля  ,

число Нуссельта .

Здесь  L, V, F, p, а, Т - соответственно длина, скорость, массовая сила, давление, скорость звука и время, характерные для данной задачи.

          Число Рейнольдса представляет собой критерий вязкости и характеризует отношение инерционных сил и сил вязкости. Число Фруда определяет отношение инерционной силы к силе тяжести. Число Струхаля характеризует отношение конвективного ускорения движения частицы к локальному ускорению и учитывает нестационарность движения. Число Маха - критерий сжимаемости, характеризует отношение инерционной силы к силе давления. Число Прандтля является мерой отношения влияния вязкости и теплопроводности.

          Используя безразмерные числа  , уравнение количества движения и неразрывности представим в следующем виде :

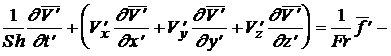
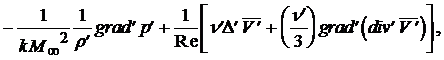
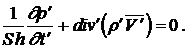
          Указанные необходимые условия являются также и достаточными для всех случаев, для которых доказана теорема существования и единственности решения дифференциальных уравнений движения вязкой жидкости.

          Числа подобия, составленные из параметров, заданных в условиях однозначности, называются критериями подобия. Из равенств критериев подобия в двух сравниваемых потоках вытекают соотношения между масштабами величин. При практическом моделировании обычно масштабы физических параметров ( например, вязкостей, плотностей жидкостей ), а также линейный масштаб задаются, а остальные масштабы вычисляются через них. Для обеспечения подобия необходимо, строго говоря, равенство чисел  Re  и  Fr  требует моделирования вязкости, что возможно лишь в исключительных случаях. Поэтому на практике моделирование выполняется по одному главному числу, обеспечивающему подобие главной ( доминирующей в данном явлении ) силы. Соответственно опыту практического моделирования для подобия потоков со свободной поверхностью ( безнапорных ) должно быть обеспечено равенство чисел Фруда, а для напорных потоков - равенство чисел Рейнольдса ( вне области квадратичного сопротивления ). Число Эйлера при моделировании потоков несжимаемой жидкости обычно является неопределяющим и зависит от чисел Re  и  Fr. Для потоков сжимаемого газа число Эйлера связано с числом Маха соотношением  . Число Маха является в большинстве случаев определяющим критерием.

          Размерные физические параметры, входящие в критерии подобия, могут принимать для подобных систем сильно различающиеся значения, одинаковыми должны быть лишь безразмерные критерии подобия. Это свойство подобных систем и составляет основу моделирования.

          Практические применения теории подобия весьма обширны. Она дает возможность предварительного качественно-теоретического анализа и выбора системы определяющих безразмерных параметров сложных физических явлений. Теория подобия является основой для правильной постановки и обработки результатов экспериментов.