Это уравнение относится к идеальной жидкости.
dx, dy, dz – размеры объема по координатным осям.
А – середина.
Дано жидкое тело, массой М, плотностью 
, которое находится в равновесии под действием внешних сил. Равнодействующую этих сил обозначим F.
Выберем декартову систему координат в которой находится тело.
Сила F может быть разложена на 3 составляющие:
F= f(Fx ;Fy; Fz)
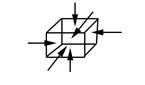Где 
- это в соответствии со 2-м законом Ньютона – проекции ускорений, вызываемых внешними силами на соответствующие координатные оси.
Выделим в жидком теле бесконечно малый объем с центром в точке А в форме прямоугольного параллелепипеда, грани которого параллельны координатным осям. Мысленно отбрасываем окружающую параллелепипед жидкую среду. Заменяем жидкую среду эквивалентными силами.
Поскольку жидкое тело находится в равновесии, соответственно и выделенный объем, то
- условие равновесия вдоль оси х.
- проекция на ось х элементарной массовой силы.
Элементарная масса прямоугольного параллелепипеда : 
- элементарный объём нашего параллелепипеда
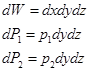
и 
- давление в точках 1 и 2.
А – центр тяжести рассматриваемого элементарного объёма .
Давление в точке А=р.
Направление оси х может быть представлено частной производной : 
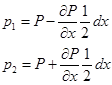
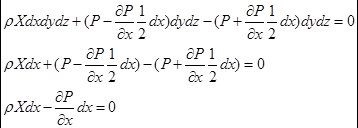
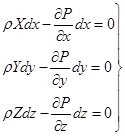
Обе части полученной системы можно разделить на константу 
и получим:
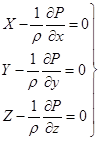
Сложим все 3 уравнения и получим следующую формулу:
- основное уравнение гидростатики.
Поможем написать любую работу на аналогичную тему