Запишем уравнение Эйлера
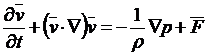 .
.
Если жидкость покоится
![]() .
.
Дифференциальные уравнения равновесия жидкости в проекции на оси декартовой системы координат могут быть записаны так
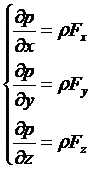 .
.
Здесь Fx, Fy, Fz - проекции на оси x,y,z сил, действующих на единицу массы рассматриваемой жидкости.
Умножая давления соответственно на dxdydz и складывая их, получаем
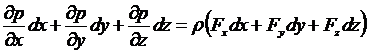 .
.
Левая часть уравнения представляет полный дифференциал
![]() ,
,
следовательно, и правая часть должна быть также полным дифференциалом, для этого необходимо и достаточно, при постоянном r, чтобы существовала функция U(x,y,z) такая что
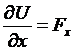 ,
, 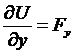 ,
, 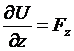 .
.
Имеем
![]() .
.
Проинтегрировав, получим
![]() ,
,
где С - постоянная интегрирования.
Если в какой-либо точке известно давление po и постоянная функция Uo, то
![]() ,
,
из интеграла имеем
![]() .
.
В частности, когда жидкость находится в поле сил тяжести
![]() ,
, ![]() ,
, ![]() .
.
Следовательно,
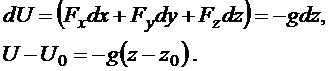
Уравнение для давления принимает вид
![]() .
.
Свободная поверхность жидкости плоская z=const. При равновесии жидкости в поле земного тяготения поверхности уровня представляют собой горизонтальные плоскости.
Рассмотрим примеры.
Пример 1. Определить уравнение свободной поверхности жидкости в сосуде, движущемся горизонтально с ускорением а.
Решение. На жидкость действуют сила тяжести и сила инерции, т.е.
![]() ,
, ![]() ,
, ![]() .
.
|
|
Имеем
откуда
- уравнение прямой. |
Следовательно, свободная поверхность представляет собой плоскость, наклоненную к горизонту под углом ![]() , который определяется из равенства
, который определяется из равенства
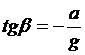 .
.
Пример 2. Определить уравнение свободной поверхности жидкости в сосуде, вращающемся вокруг вертикальной оси с угловой скоростью w .
Решение. Вследствие трения о стенки сосуда жидкость будет вращаться с такой же угловой скоростью. Жидкость будет находиться в относительном покое. Поэтому при решении задачи применимы уравнения равновесия.
|
|
Из массовых сил на жидкость действует центробежная сила и сила тяжести. Центробежная сила, действующая на массу m, находится на расстоянии r от оси вращения ( рис. 18 )
Проекции силы на оси, отнесенные к единице массы, будут
Тогда
|
Откуда
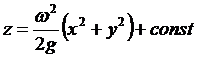 ,
,
т.е. свободная поверхность - параболоид вращения.
Поможем написать любую работу на аналогичную тему


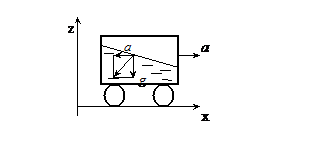 Рис. 17
Рис. 17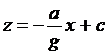
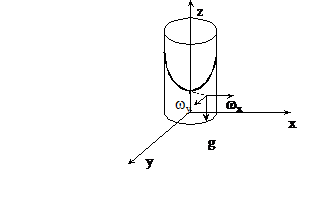 Рис. 18
Рис. 18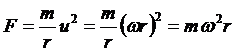 .
.