Хотя дифференциальные уравнения движения реальной жидкости справедливы также и для истинных скоростей турбулентного движения, однако сложность явлений, происходящих в нем, не позволяет для исследования этого потока воспользоваться этими уравнениями. Вместо действительного турбулентного потока в гидравлике исследуется его упрощенная модель — осредненный турбулентный поток. При построении этой модели исходят из гипотезы о том, что поле скоростей в пространстве, занимаемым турбулентным потоком, можно разбить на два поля: на поле местных осредненных скоростей u и на поле пульсационных скоростей u’.
В этом потоке проекции истинных скоростей ux, uy и uz
можно выразить через проекции осредненных скоростей 
, и 
и пульсационных 
а именно
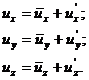
Такая модель потока позволяет установить важные соотношения между осредненными характеристиками турбулентного потока (осредненными скоростями, давлениями), что и является важнейшей задачей гидравлики.
Осредненный сформировавшийся установившийся поток, так же как и ламинарный поток в трубопроводе, формируется постепенно. Длина начального участка 6удет зависеть от условий входа и от числа Re, соответствующего потоку. Однако роль начального участка в гидравлических расчетах турбулентных потоков незначительна. Большое количество экспериментальных исследований показывает, что практически формирование поля осредненных скоростей заканчивается на длине трубопровода, равной 
.
Поможем написать любую работу на аналогичную тему