Три задачи расчёта простых трубопроводов и методы их решения.

Задача первая.

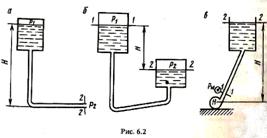
Требуется определить напор в начале трубопровода, чтобы обеспечить заданный расход жидкости Q по трубопроводу с известными параметрами. Уравнение Бернулли, записанное для сечений на поверхности жидкости в резервуаре 1-1 и на выходе из трубы 2-2 (рис. 6.2, а) имеет вид:

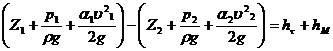
Пренебрегая величиной  в виду ее малости по сравнению с другими членами уравнения и обозначая разность высот , получим уравнение Бернулли в виде:

 где - скорость движения жидкости в трубопроводе; - абсолютные значения

Начальный искомый напор равен сумме

По заданному расходу, характеристикам жидкости (р, η) и трубопровода (I, d, ∆) находят значения v и числа Re, а также значение относительной шероховатости ∆/d , определяют режим течения, область течения и выбирают соответствующую формулу для вычисления коэффициента гидравлического сопротивления.

Аналогично решается задача, когда происходит перетекание жидкости из одного резервуара в другой (рис. 6.2, б). Для определения необходимого напора составляется уравнение Бернулли для сечений 1—1 и 2—2 на поверхностях жидкости в резервуарах. Получаем

Необходимый напор в начале трубопровода равен

Во многих случаях источником энергии для перекачки жидкости является насос. Для определения необходимого напора, создаваемого насосом в начале нагнетательной линии (рис. 6.2, в), составляется уравнение Бернулли для сечений 1—1 в начале этой линии и для сечения 2—2 на свободной поверхности жидкости в резервуаре. Принимая плоскость сравнения, проходящую через центр первого сечения, получаем

Из этого выражения может быть найдено давление , которое должен создавать насос. По найденному давлению и требуемому расходу можно выбрать соответствующий насос для перекачки жидкости. Следует отметить, что в большинстве случаев скоростным напором можно пренебречь ввиду его малости по сравнению с другими членами уравнения Бернулли.

Задача вторая.

Определение расхода жидкости заданных при остальных параметрах перекачки жидкости по трубопроводу. Рассмотрим схему подачи жидкости (см. рис. 6.2, а) в трубопровод из напорной емкости. Необходимо определить расход жидкости, что равносильно нахождению скорости движения жидкости в трубопроводе, которая входит в уравнение Бернулли.

Составим уравнение Бернулли для сечений 1 - 1 и 2—2, пренебрегая скоростными напорами:

В этой формуле левая часть может быть определена по известным данным задачи. Значение скорости, а значит и расход можно было бы найти, если есть возможность найти члены, входящие в скобки выражения (6.3). В общем случае при режимах течения, отличающихся от квадратичного, коэффициенты гидравлического сопротивления λ и местного сопротивления ζ зависят от числа Re, а значит и от ν, а вид этой зависимости заранее неизвестен. Возможны два способа решения такого типа задач: аналитический и графоаналитический.

Аналитически задача может быть решена в тех случаях, когда до начала расчета можно предсказать режим течения, а значит и вид зависимости λ от Re. Так, если предположить, что режим течения будет ламинарным, то коэффициент гидравлического сопротивления определится по формуле λ = 64/Re, а значения ζ находят по справочнику. После подготовки значений этих коэффициентов в уравнение (6.3) находят скорость v, а затем расход. Аналогично решается задача, если предполагаемый режим является квадратичным. В каждом из этих случаев требуется проверка предполагаемого режима течения, т.е. необходимо, чтобы при ламинарном течении Re < 2300, а в квадратичной зоне — Re > 500 d/∆

Если предположение не подтвердилось, то задачу решают методом последовательных приближений, задавая в первом приближении значение расхода , находят величину потерь  и сравнивают с потерями напора для заданного трубопровода, равными

Если полученное значение  оказалось больше чем , то расход уменьшают, а если меньше то следующее значение , увеличивают, последовательно приближая получаемое значение  к вычисленному .

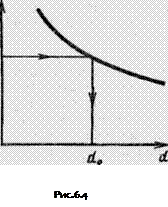
Графоаналитический метод требует построения характеристики трубопровода Q-h (зависимости потерь напора от расхода) с помощью, которой определяют расход

Для построения характеристики трубопровода сдаются рядом произвольных значений расхода жидкости  и по ним определяются потери напора  в трубопроводе, как было изложено в первой задаче. Затем по выбранным расходам и соответствующим им потерям напора строим график зависимости Q- для данного трубопровода (рис. 6.3). Для найденных потерь  по графику определяем соответствующий им расход жидкости . При решении задачи методом последовательных приближений или графоаналитическим требуется большое число вычислений, что наиболее рационально проводить с использованием ЭВМ.

Задача третья.

Определение минимально необходимого диаметра трубопровода для обеспечения заданного расхода Q при известном напоре в трубопроводе . Эта задача может быть  решена, как и в предыдущем случае аналитически, методом последовательных приближений или графоаналитически.

В последних двух случаях задаются рядом значений диаметров  и, зная Q, вычисляют потери напора . В методе последовательных приближений сравнивают получаемые значения потерь напора с заданными по условию задачи,

добиваясь их близкого совпадения.

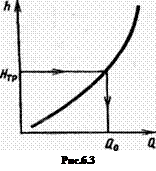
В графоаналитическом методе строится зависимость потерь напора от диаметра (рис. 6.4), а затем отложив по оси ординат предварительно вычисленные потери напора на оси абсцисс находят минимально необходимый диаметр . Если диаметр, определенный с этого графика, отсутствует в сортаменте, то берется ближайший большой диаметр.

            Рассмотрим случай последовательного соединения труб. Если трубопровод состоит из нескольких последовательно соединенных участков труб различного диаметра и различной длины (рис. 6.5), то задачи решаются изложенными способами. При этом полные потери напора на всем протяжении трубопровода определяются как сумма потерь на трение на отдельных участках и местных сопротивлений:

, а расход жидкости на каждом из участков одинаков

Равенство (6.4) выражает собой принцип наложения потерь (принцип суперпозиции).

Принцип наложения может быть использован лишь в том случае, если расстояние между имеющимися местными сопротивлениями достаточно больше. Как показали опыты, если , где L – расстояние между местными сопротивлениями, d – диаметр трубопровода, то взаимное влияние местных сопротивлений мало и в этом случае можно воспользоваться соотношением:

Если требуется найти расход в последовательно соединенном трубопроводе при задаваемых значениях 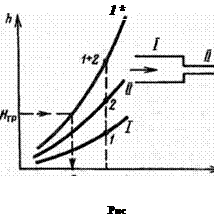напора, то в качестве расчетного служит по-прежнему соотношение: .

Если при этом заранее не известны коэффициенты λ и ζ, зависящие от расхода, то — так же как в случае простого трубопровода — эту задачу надо решать методом последовательных приближений или графоаналитическим способом. С этой целью при нескольких значениях расхода, задаваемых произвольно, строим гидравлическую характеристику для каждого участка, и совмещаем графики на одном чертеже (строим совместную характеристику), как это показано на схеме (рис. 6.6) для трубопровода, состоящего из двух участков I и II; при этом для получения точек совместной характеристики для каждого значения расхода Q суммируются соответствующие ему значения потерь напора h на каждом из участков. Таким образом, расстояние от оси абсцисс до самой верхней кривой равняется сумме потерь на всей длине трубопровода и поскольку располагаемая величина напора  известна — из графика можно определить соответствующий этому напору расход .