Методы факторного анализа экономических показателей.

Выявление взаимосвязи результативных показателей и показателей-факторов, формы зависимости между ними. Особенности применения метода элиминирования, интегрального и индексного методов. Математические методы факторного анализа.

Факторы − это условия хозяйственных процессов и причины, влияющие на них.

Факторный анализ − это методик комплексного системного изучения и измерения воздействия факторов на величину результативного показателя.

Все явления и процессы хозяйственной деятельности предприятий находятся во взаимосвязи, взаимозависимости и взаимообусловленности. Одни из них непосредственно связаны между собой, другие — косвенно. Например, на величину прибыли от основной деятельности предприятия непосредственное влияние оказывают такие факторы, как объем и структура продаж, отпускные цены и себестоимость продукции. Все другие факторы воздействуют на этот показатель косвенно. Каждое явление можно рассматривать и как причину, и как результат. Например, производительность труда можно рассматривать, с одной стороны, как причину изменения объема производства продукции, уровня ее себестоимости, а с другой — как результат изменения степени механизации и автоматизации производства, усовершенствования организации труда и т.д. Если тот или иной показатель рассматривается как следствие, как результат действия одной или нескольких причин и выступает в качестве объекта исследования, то при изучении взаимосвязей его называют результативным показателем. Показатели, определяющие поведение результативного признака, называются факторными.

Каждый результативный показатель зависит от многочисленных и разнообразных факторов. Чем детальнее исследуется влияние факторов на величину результативного показателя, тем точнее результаты анализа и оценка качества труда предприятий. Отсюда важным методологическим вопросом в анализе хозяйственной деятельности является изучение и измерение влияния факторов на величину исследуемых экономических показателей. Без глубокого и всестороннего изучения факторов нельзя сделать обоснованные выводы о результатах деятельности, выявить резервы производства обосновать планы и управленческие решения, прогнозировать результаты деятельности, оценивать их чувствительность к изменению внутренних и внешних факторов.

Под факторным анализом понимают методику комплексного и системного изучения и измерения воздействия факторов на величину результативных показателей.

Различают следующие типы факторного анализа:

•  детерминированный (функциональный) и стохастический (вероятностный);

•  прямой (дедуктивный) и обратный (индуктивный);

•  одноступенчатый и многоступенчатый;

•  статический и динамический;

•  ретроспективный и перспективный (прогнозный).

По характеру взаимосвязи между показателями различают методы детерминированного и стохастического факторного анализа.

Детерминированный факторный анализ представляет собой методику исследования влияния факторов, связь которых с результативным показателем носит функциональный характер, т.е. результативный показатель может быть представлен в виде произведения, частного или алгебраической суммы факторов.

Стохастический факторный анализ исследует влияние факторов, связь которых с результативным показателем в отличие от функциональной является неполной, вероятностной (корреляционной). Если при функциональной (полной) зависимости с изменением аргумента всегда происходит соответствующее изменение функции, то при стохастической связи изменение аргумента может дать несколько значений прироста функции в зависимости от сочетания других факторов, определяющих данный показатель. К примеру, производительность труда при одном и том же уровне фондовооруженности может быть неодинаковой на разных предприятиях. Это зависит от оптимальности сочетания всех факторов, формирующих этот показатель.

При прямом факторном анализе исследование ведется дедуктивным способом — от общего к частному. Обратный факторный анализ осуществляет исследование причинно-следственных связей способом логической индукции — от частных, отдельных факторов к обобщающим. Он позволяет оценить степень чувствительности результатов деятельности к изменению исследуемого фактора.

Факторный анализ может быть одноступенчатым и многоступенчатым. Одноступенчатый используется для исследования факторов только одного уровня (одной ступени) подчинения без их детализации на составные части. Например, у = а • b. При многоступенчатом факторном анализе проводится детализация факторов а и b на составные элементы с целью изучения их сущности. Детализация факторов может быть продолжена. В данном случае изучается влияние факторов различных уровней соподчиненности.

Необходимо различать также статический и динамический факторный анализ. Первый вид применяется при изучении влияния факторов на результативные показатели на соответствующую дату. Другой вид представляет собой методику исследования причинно-следственных связей в динамике.

И наконец, факторный анализ может быть ретроспективным, который  изучает причины изменения результатов хозяйственной деятельности за прошлые периоды, и перспективным, который исследует поведение факторов и результативных показателей в перспективе.

Основные задачи факторного анализа

1. Отбор факторов для анализа исследуемых показателей.

2. Классификация и систематизация их с целью обеспечения системного подхода.

3. Моделирование взаимосвязей между результативными и факторными показателями.

4. Расчет влияния факторов и оценка роли каждого из них в изменении величины результативного показателя.

5. Работа с факторной моделью (ее практическое использование для управления экономическими процессами).

Для изучения влияния факторов на результаты хозяйствования и подсчета резервов в анализе применяются способы детерминированного и стохастического факторного анализа, методы оптимизационного решения экономических задач (см. рисунок).

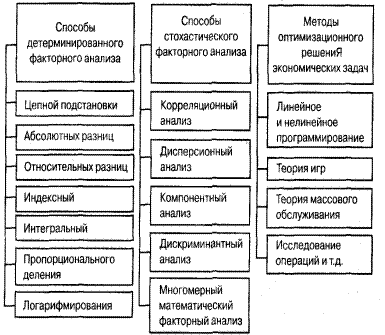
Определение величины влияния отдельных факторов на прирост результативных показателей является  одной из важнейших методологических задач в АХД. В детерминированном анализе для этого используются следующие способы: цепной подстановки, абсолютных разниц, относительных разниц, индексный, интегральный, пропорционального деления, логарифмирования, балансовый и др.

Основные свойства детерминированного подхода к анализу:

- построение детерминированной модели путем логического анализа;

- наличие полной (жесткой) связи между показателями;

- невозможность разделения результатов влияния одновременно действующих факторов, которые не поддаются объединению в одной модели;

- изучение взаимосвязей в краткосрочном периоде.

Рассмотрим возможность использования основных методов детерминированного анализа, обобщив вышеизложенное в виде матрицы

Матрица применения способов детерминированного факторного анализа

Обозначения: + используется;

– не используется

Различают четыре типа детерминированных моделей:

Аддитивные модели представляют собой алгебраическую сумму показателей и имеют вид:

К таким моделям, например, относятся показатели себестоимости во взаимосвязи с элементами затрат на производство и со статьями затрат; показатель объема производства товаров в его взаимосвязи с объемом выпуска отдельных изделий или объема выпуска в отдельных подразделениях.

Мультипликативные − это последовательное расчленение факторов исходной системы на факторы-сомножители. Модели в обобщенном виде могут быть представлены формулой:

Примером мультипликативной модели является двухфакторная модель валового выпуска продукции:                                                   ВП = ЧР * СВ

где ЧР    - среднесписочная численность работников;

       CB - среднегодовая выработка на одного работника.

Кратные модели:                                   y = x1 / x2.

Примером кратной модели служит показатель срока оборачиваемости товаров (ТОБ.Т) (в днях):                                                         ТОБ.Т = ЗТ / ОР , (1.9)

где ЗТ - средний запас товаров;

ОР - однодневный объем продаж.

Смешанные модели представляют собой комбинацию перечисленных выше моделей и могут быть описаны с помощью специальных выражений:

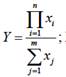
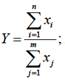
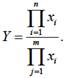
Примерами таких моделей служат показатели затрат на 1 руб. произведенной продукции, показатели рентабельности и др.

1. Наиболее универсальным из способов детерминированного анализа является способ цепной подстановки.

Он используется для расчета влияния факторов во всех типах детерминированных факторных моделей: аддитивных, мультипликативных, кратных и смешанных (комбинированных). Данный способ основан на элиминировании.

Элиминирование — это процесс поэтапного исключения воздействия всех факторов на величину результативного показателя, кроме одного. При этом исходя из того, что все факторы изменяются независимо друг от друга, т.е. сначала изменяется один фактор, а все остальные остаются без изменения. Потом изменяются два при неизменности остальных и т.д.

Этот способ позволяет определить влияние отдельных факторов на изменение величины результативного показателя. Сущность этого приема состоит в том, чтобы из всех действующих факторов выделить основные, имеющие решающее влияние на изменение показателя. С этой целью определяют ряд условных значений результативного показателя, которые учитывают изменение одного, затем двух, трех и последующих факторов, допуская, что остальные не меняются. Это означает, что в расчетах последовательно заменяют частные плановые показатели отчетными, полученные результаты сравнивают с имеющимися предыдущими данными. Сравнение значений результативного показателя до и после изменения уровня того или другого фактора позволяет элиминировать влияние всех факторов, кроме одного, и определить воздействие последнего на прирост результативного показателя.

При использовании способа цепных подстановок большое значение имеет последовательность подстановок: в первую очередь нужно учитывать изменение количественных, а затем качественных показателей. Применение обратной последовательности расчетов не дает правильной характеристики влияния факторов.

 Таким образом, применение способа цепной подстановки требует знания взаимосвязи факторов, их соподчиненности, умения правильно их классифицировать и систематизировать.

В общем виде применение способа цепных постановок можно описать следующим образом:

y0 = a0 ∙ b0 ∙ c0 ;

ya = a1 ∙ b0 ∙ c0 ;

yb = a1 ∙ b1 ∙ c0 ;

y1 = a1 ∙ b1 ∙ c1 ;

где a0, b0, c0 - базисные значения факторов, оказывающих влияние на обобщающий показатель у;

a1 , b1, c1 - фактические значения факторов;

ya, yb,    - промежуточные значения результирующего показателя, связанного с изменением факторов а и b, соответственно.

Общее изменение Δу = у1 – у0 складывается из суммы изменений результирующего показателя за счет изменения каждого фактора при фиксированных значениях остальных факторов. Т.е. сумма влияния отдельных факторов должна равняться общему приросту результативного показателя.

∆y = ∆ya + ∆yb + ∆yc = y1– y0

∆ya = ya – y0 ;

∆yb = yb – ya ;

∆yc = y1 – yb  .

Преимущества данного способа: универсальность применения, простота расчетов.

Недостаток метода состоит в том, что, в зависимости от выбранного порядка замены факторов, результаты факторного разложения имеют разные значения.

2. Способ абсолютных разниц является модификацией способа цепной подстановки.

Способ абсолютных разниц применяется для расчета влияния факторов на прирост результативного показателя в детерминированном анализе, но только в мультипликативных моделях (Y = х1 ∙ х2 ∙ х3 ∙∙∙∙∙ хn) и моделях мультипликативно-аддитивного типа: Y = (а - b)∙с и Y = а∙(b - с). И хотя его использование ограничено, но благодаря своей простоте он получил широкое применение в АХД.

Суть метода способа − величина влияния факторов рассчитывается путем умножения абсолютного прироста значения исследуемого фактора на базовую (плановую) величину факторов, которые находятся справа от него, и на фактическую величину факторов, расположенных в модели слева от него.

  y0 = a0 ∙ b0 ∙ c0

∆ya = ∆a ∙ b0 ∙ c0

∆yb = a1 ∙ ∆b ∙ c0

∆yс = a1 ∙ b1 ∙ ∆с

  y1 = a1 ∙ b1 ∙ c1

Алгебраическая сумма прироста результативного показателя за счет отдельных факторов должна равняться его общему изменению Δу = у1 – у0.

∆y = ∆ya + ∆yb + ∆yc = у1 – у0

Рассмотрим алгоритм расчета факторов этим способом в моделях мультипликативно-аддитивного вида. Для примера возьмем факторную модель прибыли от реализации продукции:

П = VРП ∙ (Ц − С),

где П      − прибыль от реализации продукции;

      VРП  − объем реализации продукции;

      Ц       − цена единицы продукции;

      С     − себестоимость единицы продукции.

Прирост суммы прибыли за счет изменения:

объема реализации продукции       ∆ПVРП = ∆VРП ∙ (Ц0 − С0);

иены реализации                            ∆ПЦ = VРП1 ∙ ∆Ц ;

себестоимости продукции              ∆ПС = VРП1 ∙ (−∆С);

3. Способ относительных разниц Он используется в случаях, когда исходные данные содержат определенные ранее относительные отклонения факторных показателей в процентах. Применяется для измерения влияния факторов на прирост результативного показателя только в мультипликативных моделях. Здесь используются относительные приросты факторных показателей, выраженные в виде коэффициентов или процентов. Рассмотрим методику расчета влияния факторов этим способом для мультипликативных моделей типа Y = abc.

Изменение результативного показателя определяется следующим образом:

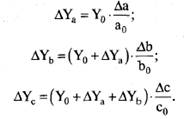
Согласно данному алгоритму для расчета влияния первого фактора необходимо базовую величину результативного показателя умножить па относительный прирост первого фактора, выраженного в виде десятичной дроби.

Чтобы рассчитать влияние второго фактора, нужно к базовой величине результативного показателя прибавить изменение его за счет первого фактора и затем полученную сумму умножить на относительный прирост второго фактора.

Влияние третьего фактора определяется аналогично: к базовой величине результативного показателя необходимо прибавить его прирост за счет первого и второго факторов и полученную сумму умножить на относительный прирост третьего фактора и т.д.

Результаты расчетов такие же, как и при использовании предыдущих способов.

Способ относительных разниц удобно применять в тех случаях, когда требуется рассчитывать влияние большого комплекса факторов (8-10 и более). В отличие от предыдущих способов здесь значительно сокращается число вычислительных процедур, что обусловливает его преимущество.

4. Интегральный метод оценки факторных влияний позволяет избежать недостатков, присущих методу цепной подстановки, и не требует применения приемов по распределению неразложимого остатка по факторам, т.к. в нем действует логарифмический закон перераспределения факторных нагрузок. Интегральный метод позволяет достигнуть полного разложения результативного показателя по факторам и носит универсальный характер, т.е. применим к мультипликативным, кратным и смешанным моделям. Операция вычисления определенного интеграла осуществляется с помощью вычислительных возможностей персональных компьютеров и сводится к построению подынтегральных выражений, которые зависят от вида функции или модели факторной системы.

Его использование позволяет получать более точные результаты расчета влияния факторов по сравнению со способами цепной подстановки, абсолютных и относительных разниц, поскольку дополнительный прирост результативного показателя от взаимодействия факторов присоединяется не к последнему фактору, а делится поровну между ними.

Рассмотрим алгоритмы расчетов влияния факторов для разных моделей:

1) Модель вида: y = a ∙ b

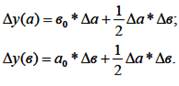
2) Модель вида: y = a ∙ b ∙ с

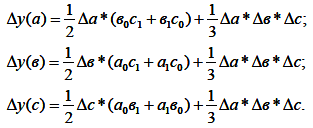
3) Модель вида:

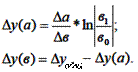
3) Модель вида:

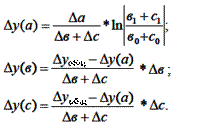
Если в знаменателе больше двух факторов, то процедура продолжается.

Таким образом, использование интегрального метода не требует знания всего процесса интегрирования. Достаточно в эти готовые рабочие формулы подставить необходимые числовые данные и сделать не очень сложные расчеты с помощью калькулятора или другой вычислительной техники.

Результаты расчетов по интегральному методу существенно отличаются от того, что дает метод цепных подстановок или модификации последнего. Чем больше величина изменений факторов, тем разница значительнее.

5. Индексный метод позволяет выявить влияние на изучаемый совокупный показатель различных факторов. Рассчитав индексы и построив временной ряд, характеризующий, например, выпуск продукции в стоимостном выражении, можно квалифицированно судить о динамике объема производства.

Основывается на относительных показателях динамики, выражающих отношение уровня анализируемого показателя в отчетном периоде к его уровню в базисном периоде. Индексным методом можно

Всякий индекс исчисляется сопоставлением соизмеряемой (отчетной) величины с базисной. Например, индекс объема производства:  Ivвп = VВП1 / VВП0

Индексы, выражающие соотношение непосредственно соизмеряемых величин, называются индивидуальными, а характеризующие соотношения сложных явлений — групповыми, или тотальными. Статистика называет несколько форм индексов, которые используются в аналитической работе − агрегатная, арифметическая, гармоническая и др.

Применяя агрегатную форму индекса и соблюдая установленную вычислительную процедуру, можно решить классическую аналитическую задачу: определение влияния на объем произведенной или реализованной продукции фактора количества и фактора цен. Схема расчета при этом будет такой:

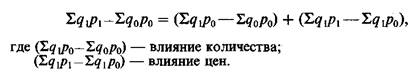
Здесь следует напомнить, что агрегатный индекс является основной формой всякого общего индекса; его можно преобразовать как в средний арифметический, так и в средний гармонический индексы.

Динамика оборота по реализации промышленной продукции должна характеризоваться, как известно, временными рядами, построенными за ряд истекших лет с учетом изменения цен (это относится, естественно, к заготовительному, оптовому и розничному оборотам).

Индекс объема реализации (товарооборота), взятый в ценах соответствующих лет, имеет вид:

Общий индекс цен: 

Общие индексы — относительные показатели, получаемые в результате сравнения явлений, охватывающих неоднородные товарные группы.

Общий индекс товарооборота (стоимости товарной продукции);

Iqp =

где p1q1 − товарооборот отчетного периода

p0q0 − товарооборот базисного периода

p − цены,  q − количество

Общий индекс цен:                                   Ip =

Средние индексы — это относительные показатели, применяемые для анализа структурных изменений. Они используются только для однородных товаров.

Индекс цен переменного состава (средних цен):

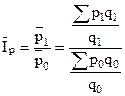
Индекс цен постоянного состава:

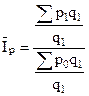
6. Способ пропорционального деления может быть использован в ряде случаев для определения величины влияния факторов на прирост результативного показателя. Это касается тех случаев, когда мы имеем дело с аддитивными моделями Y=∑хi и моделями кратно-аддитивного типа:

В первом случае, когда имеем одноуровневую модель типа Y= а + b + с, расчет проводится следующим образом:

В моделях кратно-аддитивного типа сначала необходимо способом цепной подстановки определить, насколько изменился результативный показатель за счет числителя и знаменателя, а затем произвести расчет влияния факторов второго порядка способом пропорционального деления по вышеприведенным алгоритмам.

Например, уровень рентабельности повысился на 8% в связи с увеличением суммы прибыли на 1000 тыс. руб. При этом прибыль возросла за счет увеличения объема продаж на 500 тыс. руб., за счет роста цен — на 1700 тыс. руб., а за счет роста себестоимости продукции снизилась на 1200 тыс. руб. Определим, как изменился уровень рентабельности за счет каждого фактора:

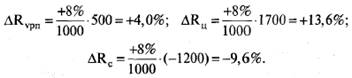
7. Для решения такого типа задач можно использовать также способ долевого участия. Для этого сначала определяется доля каждого фактора в общей сумме их приростов (коэффициент долевого участия), которая затем умножается на общий прирост результативного показателя (табл. 4.2):

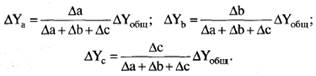
Расчет влияния факторов на результативный показатель способом долевого участия

8. В основе приема последовательного изолирования факторов лежит метод научной абстракции, позволяющий исследовать большое число комбинаций с одновременным изменением всех или части факторов.