Основы финансовой математики: временная стоимость денег (наращение и дисконтирование), простой и сложный процент, начисление процентов за дробное число лет, непрерывное начисление процентов, эффективная годовая процентная ставка

Временную ценность. Этот параметр можно рассматривать в двух аспектах.

Первый аспект связан с обесценением денежной наличности с течением времени.

Второй аспект связан с обращением капитала (денежных средств).

Проблема «деньги—время» не нова, поэтому уже разработаны удобные модели и алгоритмы, позволяющие ориентироваться в истинной цене будущих доходов с позиции текущего момента. Коротко охарактеризуем их в теоретическом и практическом аспектах.

Логика построения основных алгоритмов достаточно проста и основана на следующей идее. Простейшим видом финансовой сделки является однократное предоставление в долг некоторой суммы РV с условием, что через некоторое время / будет возвращена большая сумма FV. Как известно, результативность подобной сделки может быть охарактеризована двояко: либо с помощью абсолютного показателя — прироста (FV - РV), либо путем расчета некоторого относительного показателя. Абсолютные показатели чаще всего не подходят для подобной оценки ввиду их несопоставимости в пространственно-временном аспекте. Поэтому пользуются специальным коэффициентом — ставкой. Этот показатель рассчитывается отношением приращения исходной суммы к базовой величине, в качестве которой, очевидно, можно взять либо РV, либо FV. Таким образом, ставка рассчитывается по одной из двух формул:

В финансовых вычислениях первый показатель имеет еще названия «процентная ставка», «процент», «рост», «ставка процента», «норма прибыли», «доходность», а второй — «учетная ставка», «дисконт». Очевидно, что обе ставки взаимосвязаны, т.е. зная одни показатель, можно рассчитать другой

Оба показателя могут выражаться либо в долях единицы, либо в процентах. Различие в этих формулах состоит в том, какая величина берется за базу сравнения: в формуле (7.1)—исходная сумма, в формуле (7.2) — возвращаемая сумма

Процесс, в котором заданы исходная сумма и ставка (процентная или учетная), в финансовых вычислениях называется процессом наращения, искомая величина — наращенной суммой, а используемая в операции ставка — ставкой наращения. Процесс, в котором заданы ожидаемая в будущем к получению (возвращаемая) сумма и ставка, называется процессом дисконтирования, искомая величина — приведенной суммой, а используемая в операции ставка — ставкой дисконтирования. В первом случае речь идет о движении денежного потока от настоящего к будущему, во втором — о движении от будущего к настоящему (рис. 7.1).

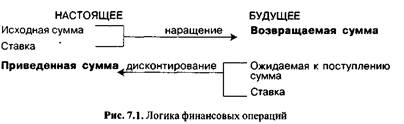
Экономический смысл финансовой операции, задаваемой формулой (7.1), состоит в определении величины той суммы, которой будет или желает располагать инвестор по окончании этой операции. Из формулы (7.1)

Разность I =FV— РV называется процентом. Это величина дохода от предоставления в долг денежной суммы РV.

Предоставляя денежные средства в долг, их владелец получает определенный доход в виде процентов, начисляемых по некоторому алгоритму в течение определенного промежутка времени. Поскольку стандартным временным интервалом в финансовых операциях является 1 год, наиболее распространен вариант, когда процентная ставка устанавливается в виде годовой ставки, подразумевающей однократное начисление процентов по истечении года после получения ссуды. Известны две основные схемы дискретного начисления:

схема простых процентов (simple interest);

схема сложных процентов (compound interest).

Схема простых процентов предполагает неизменность базы, с которой происходит начисление. Пусть исходный инвестируемый капитал равен Р; требуемая доходность — r (в долях единицы). Считается, что инвестиция сделана на условиях простого процента, если инвестированный капитал ежегодно увеличивается на величину Р*r. Таким образом, размер инвестированного капитала (Rn) через n лет будет равен:

Rn =Р + Р- г + ...+Р- r = P- (1 + n • г).           (7.3)

Считается, что инвестиция сделана на условиях сложного процента, если очередной годовой доход исчисляется не с исходной величины инвестированного капитала, а с общей суммы, включающей также и ранее начисленные и не востребованные инвестором проценты. В этом случае происходит капитализация процентов по мере их начисления, т.е. база, с которой начисляются проценты, все время возрастает. Следовательно, размер инвестированного капитала будет равен:

к концу первого года: F1 = P + P*r = P(1+ r);

к концу второго года: F2= F1 + F1 * r= F1 • (1 + r) = Р • (1 + r)2;

к концу n-го года: Fn = Р (1 + r)n.

Как же соотносятся величины Rn и Fn? Это чрезвычайно важно знать при проведении финансовых операций. Все зависит от величины п. Сравним множители наращения по простым и сложным процентам, т.е. сравним: 1 + п *r и (1 + r)n. Очевидно, что при п = 1 эти множители совпадают и равны 1 + r. Можно показать, что при любом r справедливы неравенства: 1 + п * r > (1 + r)n , если 0 < п < 1 и 1 + п * r > (1 + r)n, если и > 1. Итак,

Rn > Fn npn O<n< 1;

Rn < Fn  при n > 1.

Графически взаимосвязь Fn и Rn  можно представить следующим образом (рис. 7.2).

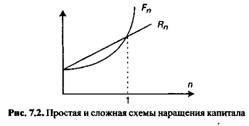
Таким образом, в случае ежегодного начисления процентов для лица, предоставляющего кредит:

более выгодной является схема простых процентов, если срок ссуды менее одного года (проценты начисляются однократно в конце периода);

более выгодной является схема сложных процентов, если срок ссуды превышает один год (проценты начисляются ежегодно);

обе схемы дают одинаковые результаты прн продолжительности периода одни год и однократном начислении процентов.

В случае краткосрочных ссуд со сроком погашения до одного года в качестве показателя «берется величина, характеризующая удельный вес длины подпериода (дни, месяц, квартал, полугодие) в общем периоде (год). /Длина различных временных интервалов в расчетах может округляться: месяц — 30 дней; квартал — 90 дней; полугодие — 180 дней; год — 360 (илн 365,366) дней.

Определяя продолжительность финансовой операции, принято день выдачи и день погашения ссуды считать за один день. В зависимости от того, чему берется равной продолжительность (года, квартала, месяца), размер промежуточной процентной ставки может быть различным. Возможны два варианта:

точный процент, определяемый исходя из точного числа дней в году (365 или 366), в квартале (от 89 до 92), в месяце (от 28 до 31);

обыкновенный процент, определяемый исходя из приближенного числа дней в году, квартале и месяце (соответственно 360, 90, 30).

При определении продолжительности периода, иа который выдана ссуда, также возможны два варианта:

принимается в расчет точное число дней ссуды (расчет ведется по дням);

принимается в расчет приблизительное число дней ссуды (исходя из продолжительности месяца в 30 дней).

В том случае, когда в расчетах используется точный процент, берется и точная величина продолжительности финансовой операции; при использовании обыкновенного процента может применяться как точное, так и приближенное число дней, на которые получены ссуды

Достаточно обыденными являются финансовые контракты, заключаемые на период, отличающийся от целого числа лет. В этом случае проценты могут начисляться одним нз двух методов:

• по схеме сложных процентов:

• по смешанной схеме (используется схема сложных процентов для целого числа лет и схема простых процентов — для дробной части года):

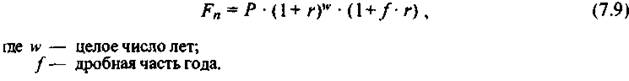Поскольку f< 1, то (1 +f* r) > (1 +r)f, следовательно, наращенная сумма будет больше при нспользованнн смешанной схемы. Можно показать, что прн малых r наибольшая величина разности между (7.9) и (7.8) достигается прн f =0,5.

Все рассмотренные ранее начисляемые проценты называются дискретными, поскольку их начисление осуществляется за фиксированный промежуток времени (год, квартвл, месяц, день, даже час). Уменьшая этот промежуток (период начисления) и увеличивая частоту начисления процентов, в пределе можно перейти к так называемым непрерывным процентам.

Уже отмечалось, что в зависимости от частоты начисления процентов наращение суммы осуществляется различными темпами, причем с возрастанием частоты накопленная сумма увеличивается. Максимально возможное наращение осуществляется при бесконечном дроблении годового интервала. Из формулы (7.7) следует

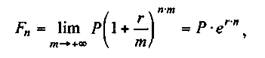
Чтобы отличить непрерывную ставку от обычной (дискретной), вводят специальное обозначение непрерывной ставки — д, и называют ее силой роста. Таким образом, формула для нахождения наращенной суммы за п лет при непрерывном начислении процентов принимает вид;

Fn =Редп

где е6п является множителем иаращеиия, причем этой формулой пользуются и в тех случаях, когда п не является целым числом.

Таким образом, прн непрерывном начислении процентов в пределах одного года используется следующая базовая формула:

F1 =Р * е6

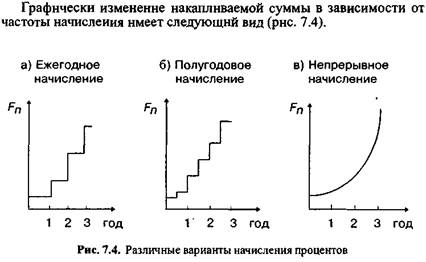
Различными видами финансовых контрактов могут предусматриваться различные схемы начисления процентов. Как правило, в этих контрактах оговаривается номинальная процентная ставка, обычно годовая. Эта ставка, во-первых, не отражает реальной эффективности сделки и, во-вторых, не может быть использована для сопоставлений. Для того чтобы обеспечить сравнительный анализ эффективности таких контрактов, необходимо выбрать некий показатель, который был бы универсальным для любой схемы начисления. Таким показателем является эффективная годовая процентная ставка re, обеспечивающая переход от Р к Fn при заданных значениях этих показателей и однократном начислении процентов.

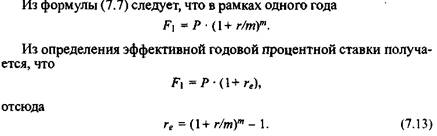Общая постановка задачи может быть сформулирована следующим образом. Задана исходная сумма Р, годовая процентная ставка (номинальная) r, число начислений сложных процентов т. Этому набору исходных величин в рамках одного года соответствует вполне определенное значение наращенной величины F1. Требуется найти такую годовую ставку re, которая обеспечила бы точно такое же наращение, как и исходная схема, но прн однократном начислении процентов, т.е. m = 1. Иными словами, схемы {Р, F1, r, т> 1} и {P, F1, re, т = 1} должны быть равносильными.

Из формулы (7.13) следует, что эффективная ставка зависит от количества внутрнгодовых начислений, причем с ростом т она увеличивается. Кроме того, для каждой номинальной ставки можно найти соответствующую ей эффективную ставку; две эти ставки совпадают лишь прн т = 1. Именно ставка rе является критерием эффективности финансовой сделки и может быть использована для пространственно-временных сопоставлений.