ПОСТАНОВКА ЗАДАЧИ ОПТИМИЗАЦИИ

Математическая постановка задачи оптимизации учитывает:

• множество А условий функционирования и состояния внешней среды А: а;

•      совокупность ограничений на структуру s и параметры и анализируемой системы (U - множество допустимых реализаций параметров, S - множество возможных структур);

•      множество показателей качества (ПК) системы Р= {pi ,...,pn};

•      совокупность критериальных ограничений (Q - множество допустимых комбинаций показателей).

Конкретная реализация каждого из этих компонентов зависит от таких факторов, как иерархический уровень оптимизируемой системы, объем и достоверность априорной информации, сопоставимость различных ПК. В общем виде задача векторного синтеза может быть сформулирована в виде

                                                              (1.1)

Ее решение существенно зависит от трактовки понятия оптимальности, количества и достоверности информации о компонентах задачи (1.1), включая ограничения. Задачу векторной оптимизации (1.1) можно решать в следующей последовательности:

•      определить допустимые варианты построения системы;

•      выявить основные ПК сравниваемых систем;

•      определить "нехудшие" системы на основании критерия безусловного предпочтения Парето;

•      привести показатели не сравнимых по Парето систем к сопоставимому виду;

•      выбрать оптимальное решение.

Для выбора "нехудших" систем (оптимальных по Парето) разработаны достаточно эффективные методы. Но, как правило, методы безусловного предпочтения не позволяют окончательно определить оптимальное решение. В связи с этим предложен ряд методов векторной оптимизации, среди которых следует отметить методы выделения ведущего показателя, лексикографического упорядочения показателей, использования принципа гарантированного результата и его обобщений, а также методы последовательных уступок, формирования обобщенного ПК (ОПК) и др.

При наличии возрастающего ОПК  W(рi, ..., р„) задача векторного синтеза (1.1) примет вид

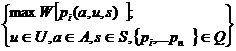                                         (1.2)

и сведется к задаче скалярного синтеза. Для ее решения могут быть использованы традиционные методы решения условно-экстремальных задач.