Электростатическое поле вблизи заряженных поверхностей (граничные условия).

Рассмотрим тонкую поверхность, т.е. при любом выборе пощади площади S толщина поверхности h много меньше чем . Пусть - поверхностная плотность заряда.

Исследуем особенности электростатического поля сверху и снизу от поверхности. В общем случае функция поля  может быть любой, даже разрывной.

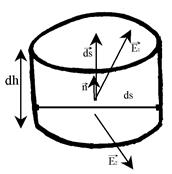
Выберем на поверхности площадку, на столько малую, что её можно считать частью плоскости, а электрическое поле сверху и снизу от неё не изменяются (сверху и снизу поля разные, но постоянные).

Выберем замкнутую поверхность в виде цилиндра так, чтобы его основания были параллельны площадке. Поскольку цилиндрик на столько мал, что вектора и на его поверхности постоянны, то поток электростатического поля  через него можно записать следующим образом , где  и  проекции векторов и  на перпендикуляр к площадке, - поток через боковую поверхность цилиндра. Теперь будем уменьшать высоту  цилиндра  , т.к. .

По теореме Гаусса , где  - заряд на площадке, откуда . Итак, при переходе через поверхность нормальная компонента вектора  испытывает скачок, равный  с точностью до константы .

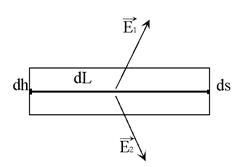
Найдем соотношение для тангенциальной компоненты вектора  при переходе через поверхность. Опять же выберем на поверхности площадку, на столько малую, что её можно считать частью плоскости, а электрическое поле сверху и снизу от неё не изменяются (сверху и снизу поля разные, но постоянные). Теперь выберем замкнутый контур виде прямоугольника т.о., чтобы площадка  его пересекала под прямым углом. Длины сторон прямоугольника, параллельных площадке равны , а боковые. Запишем циркуляцию вектора  по замкнутому контуру , где  и  - тангенциальные составляющие вектора  к площадке.  тангенциальная составляющая вектора  всегда непрерывна.

Соотношения  и  называются граничными условиями.

Пример1.

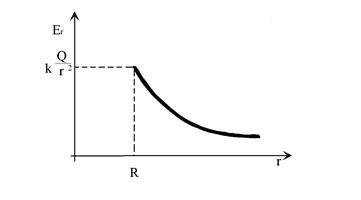
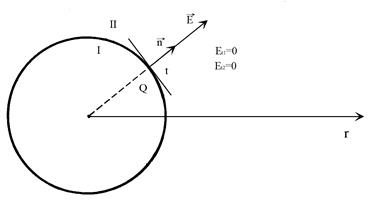Проверим, выполняются ли граничные условия для равномерно заряженной сферы. Знаем, что поле сферы равно .

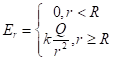Поле на сфере всегда направленно по нормали к поверхности, поэтому все тангенциальные компоненты вектора  равны нулю.

Поле внутри сферы равно нулю, поэтому . А вне сферы . Граничные условия выполняются.

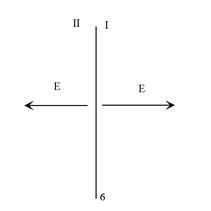Пример2. Бесконечная заряженная плоскость.

Обе тангенциальные компоненты вектора  равны нулю, они непрерывны. Разность нормальных компонент вектора равна .

Граничные условия помогают решать некоторые задачи.