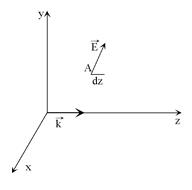
Рассмотрим в пространстве произвольное электростатическое поле. Введем декартовую систему координат. Зафиксируем некоторую точку А и построим вокруг неё меленький кубик, на столько маленький, что внутри него не меняется поле и объёмная плотность заряда. Его ребра параллельны осям координат и называются 
, 
и 
.
Поместим туда единичный положительный заряд с посчитаем работу по его перемещению вдоль оси 
на . Эта работа равна 
, где 
-орт. Из этого равенства получим следующее соотношение 
. Проделав ту же операцию по другим координатам получим: 
, 
. Теперь сконструируем вектор
Теперь вспомним т. Гаусса в дифференциальной форме: 
Дивергенция вектора 
выражается следующим образом: 
, а дивергенция от градиента потенциала:
, где
-- оператор Лапласа (лапласиан) обозначается символами 
, или 
. Итак, получается, что в электростатике справедлива следующая формула: 
видим, что потенциал определяется через объёмную плотность заряда в точке. Это уравнение можно решить в очень ограниченном числе случаев.
Следует заметить частный случай, когда мы рассматриваем точку, в которой нет зарядов, но рядом может находиться заряженное тело, тогда в этой точке 
.
Поможем написать любую работу на аналогичную тему