Теорема Гаусса для электрических полей.

Рассмотрим некоторую поверхность , в которой имеется электрическое поле. Выберем на поверхности  малую площадку , настолько малую, что ее можно считать частью плоскости. Построим нормаль к этой площадке.

.

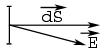
Пусть  настолько мало, что вектор электрического поля на  постоянен. Введем величину .

.

Величина  называется потоком вектора  через площадку . Если мы разобьем все поверхность  на площадки  и их просуммируем, то получим поток вектора  через поверхность .

.

Теорема Гаусса: поток вектора  через замкнутую поверхность  равен

,

где  – полный заряд, содержащийся внутри поверхности .

Доказательство.

1.     Точечный заряд и поверхность в виде сферы с центром в точечном заряде.

Поскольку модуль вектора напряженности поля точечного заряды определяется , то модуль вектора напряженности во всех точках сферы постоянен. Из закона Кулона следует, что вектор напряженности направлен по радиусу.

.

2.     Точечный заряд и произвольная поверхность, окружающая точечный заряд.

Выберем площадку  на поверхности. Она должна быть настолько мала. Чтобы можно было ее считать плоскостью и вектор напряженности электрического поля на ней считать постоянным.

,

где  – конус, под которым  из точки  можно увидеть выбранную площадку.

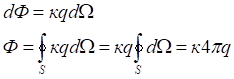
3.     Заряженное тело внутри произвольной поверхности.

Разобьем заряженное тело на множество кусочков, удовлетворяющих второму постулату. Введем функцию плотности заряда . По доказанному выше следует, что для каждого точечного заряда теорема Гаусса выполняется.

где .

.

Замечания.

1.     Теорема Гаусса выглядит так замечательно потому, что поле обратнопропорционально .

2.     для гравитационного поля тоже можно записать теорему Гаусса.

Пример1. Поле заряженной сферы.

 – радиус сферы,  – заряд, равномерно распределенный по поверхности сферы .

1.               

Выберем точку, находящуюся на расстоянии от центра сферы. Окружим сферу воображаемой поверхностью, проходящей через эту точку, и для нее запишем теорему Гаусса. Поле выбранной поверхности симметрично, так как симметрично поле источника.

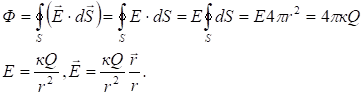
Большая сфера создает такое же поле, как и точечный заряд.

Примеры:

1.     Рассчитаем поле заряженной сферы. Пусть есть заряженная сфера радиуса R с положительным зарядом Q, найдем электростатическое поле этой сферы на некотором расстоянии r от её центра. Пусть . Проведем сферу S радиуса r с центром в центре заряженной сферы.

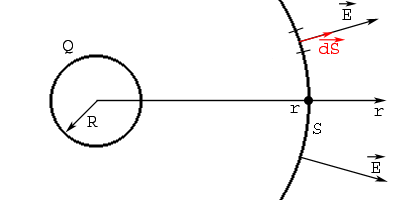
 В силу симметричности задачи очевидно, что поле создаваемое заряженной сферой на сфере радиуса r везде одинаково по модулю и направлено по радиусу. Тогда поток через эту сферу запишется так:

.

Откуда - . Т.е. заряженная сфера создаёт вне себя такое же поле как и такой же точечный заряд находящийся в центре этой сферы

Пусть .

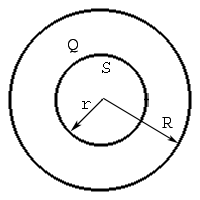
Тогда поток через эту сферу запишется так:

.

Откуда - . Т.е. поля внутри заряженной сферы нет.

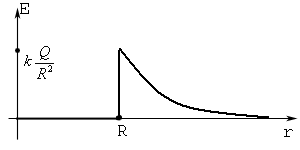
2.     Рассмотрим поле бесконечной, однородной, тонкой, заряженной плоскости.

Выберем площадку  с зарядом .  - поверхностная плотность заряда.  - общий случай. Если  то плоскость однородно заряженная. Рассмотрим однородно заряженную плоскость, с плотностью заряда . Выберем на ней некоторое , малое настолько, что  можно считать постоянным. Рассмотрим параллелепипед S, такой что его верхние грани параллельны заряженной плоскости и по площади равны , а боковые грани разделены заряженной плоскостью пополам (ребро боковой грани 2h).

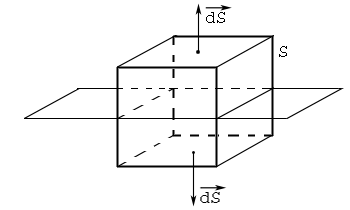
Тогда поток через этот параллелепипед равен

.

Рассмотрим некоторую точку не лежащую на данной плоскости. Опустим из неё перпендикуляр на данную плоскость и от полученной точки отсчитаем в разные стороны симметричные полоски одинаковой длины, малые настолько, что создаваемое ими поле можно считать одинаковым.

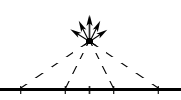
Проссумируем попарно напряженности от всех полосок. Из элементарной геометрии очевидно, что  располагается по нормали к плоскости. Тогда =0, т.к. вектор площади боковой поверхности перпендикулярен напряженности. Но очевидно, что . Откуда

.

.

Т.о. поле зависит только от  и по модулю одинаково в каждой точке.

3.  Найдем поле 2-х заряженных бесконечных плоскостей.

Пусть обе плоскости заряжены одинаково. По принципу суперпозиции обе плоскости действуют независимо.

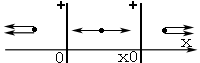
1) : ;

2) : ;

3) : .

Пусть обе плоскости заряжены разноимённо.

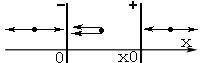
1) : ;

2) : ;

3) : .

Замечания:

1.     Бесконечных плоскостей нет. Но заряженную плоскость можно считать бесконечной если расстояние до исследуемой точки много меньше чем характерные размеры плоскости ().

2.     В каждом случае E разрывна (т.е. испытывает скачок).

3.     Теорема Гаусса справедлива всегда, но использовать её можно только для решения симметричных задач.

4.     Теорема Гаусса – синтез закона Кулона и принципа суперпозиции.