Теорема Гаусса - Остроградского для поля в диэлектрике. Связь векторов  - смещения,  - напряженности и  - поляризованности - Лекции по электростатике

Теорема Гаусса - Остроградского для потока вектора  в вакууме имела вид:

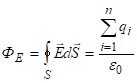                                      ,   или      

где Q - суммарный заряд, охватываемый замкнутой поверхностью S. В диэлектрике Q складывается из свободных (сторонних) зарядов и связанных зарядов, т.е.

                                           (5)

Можно показать, что                               .

Подставляя эту формулу в (5), после преобразования получим

                                           (6)

Величину                                                                                                                         (7)

называют вектором электрического смещения или вектором электрической индукции. Она измеряется, как и , в Кл/м2. Учитывая, что          находим

   .                             (8)

Линии вектора  могут начинаться или заканчиваться лишь на свободных зарядах, а линии  - на свободных и связанных. С учетом (7) формула (6) запишется так

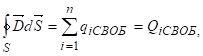                                                  ,                                               (9)

т.е. поток вектора электрического смещения через произвольную замкнутую поверхность S  равен алгебраической сумме свободных зарядов, охватываемых этой поверхностью.

Это и есть теорема Гаусса - Остроградского в интегральной форме для поля в диэлектрике, которая в дифференциальной форме выглядит так:               

                                                      = dq/dV,   Кл / м                           (10)

ρ – объемная плотность свободных зарядов.