Поток вектора напряженности. Теорема Остроградского-Гаусса для электрического поля в вакууме

Поток вектора напряжённости электрического поля через любую произвольно выбранную замкнутую поверхность пропорционален заключён-ному внутри этой поверхности электрическому заряду.

 Если имеется поле некоторого вектора А, то выражение

Ф=

где Аn — составляющая вектора А по направлению нормали к dS, называется потоком вектора А через поверхность S.

В зависимости от природы вектора А выражение имеет различный физический смысл. Так, например, поток вектора плотности потока энергии равен, как известно, потоку энергии через соответствующую поверхность

Поток вектора скорости  дает объем жидкости, протекающей в единицу времени через поверхность S

Ф=

Из формулы следует, что поток вектора Е численно равен количеству линий Е, пронизывающих поверхность S.

Ф=

Пусть внутри некоторой замкнутой поверхности заключено несколько точечных зарядов произвольных знаков: q 1, q2 и т. д. Поток вектора Е по определению равен

Ф=

(кружок у знака интеграла указывает на то, что интегрирование производится по замкнутой поверхности).

В силу принципа суперпозиции полей

Еn = Еn1 + Еn2 + ... =∑Еi         

Подставив в выражение для потока, получим

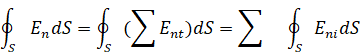
где Еni — нормальная составляющая напряженности поля, создаваемого i-м зарядом в отдельности.

Но, как было показано выше,

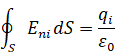
Следовательно,

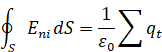
Доказанное нами утверждение носит название теоремы Гаусса. Эта теорема может быть сформулирована следующим образом: поток вектора напряженности электрического поля через замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на εо.

В частности, если внутри поверхности заряды отсутствуют, поток равен нулю.