Сторонние силы. Э.д.с. и напряжение

Если в цепи, на носители тока действуют только силы электростатического поля, то происходит перемещение носителей от точек с большим потенциалом к точкам с меньшим потенциалом. Это приведет к выравниванию потенциалов во всех точках цепи и к исчезновению электрического поля. Поэтому для существования постоянного тока необходимо наличие в цепи устройства, способного создавать и поддерживать разность потенциалов за счет работы сил неэлект-тростатического происхождения. Такие устройства называются источниками тока. Силы неэлектростатического происхождения, действующие на заряды со стороны источников тока, называются сторонними.

Сторонние силы совершают работу по перемещению электрических зарядов. Физическая величина, определяемая работой, совершаемой сторонними силами при перемещению единичного положительного заряда, называется электродвижущей силой (э.д.с.) действующей цепи:

.                                                             

Сторонняя сила Э.Д.С. , действующая на заряд Q0 может быть выражена как

Работа же сторонних сил по перемещению заряда Q0 на замкнутом участке цепи равна

.                                

Разделив (97.2) на Q0, получим выражение для Э.Д.С.., действующей в цепи:

.

Э.Д.С., действующая на участке 1—2, равна

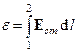
На заряд Q0 помимо сторонних сил действуют также силы электростатического поля Fe=Q0E. Таким образом, результирующая сила, действующая в цепи на заряд Q0 равна

.

Работа, совершаемая результирующей силой над зарядом Q0 на участке 1—2, равна

.                                     

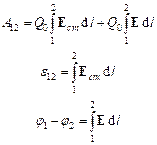
Для замкнутой цепи работа электростатических сил равна нулю, поэтому в данном случае .

Напряжением U на участке 1—2 называется физическая величина, определяемая работой, совершаемой суммарным полем электростатических (кулоновских) и сторонних сил при перемещении единичного положительного заряда на данном участке цепи. Таким образом, согласно (97.4),

Понятие напряжения является обобщением понятия разности потенциалов: напряжение на концах участка цепи равно разности потенциалов в том случае, если на этом участке не действует Э.Д.С., т. е. сторонние силы отсутствуют.

Закон Ома. Сопротивление проводников.

Сила тока I, текущего по однородному металлическому проводнику (т. е. проводнику, в котором не действуют сторонние силы), пропорциональна напряжению U на концах проводника:

.                                                          

Уравнение (98.1) выражает закон Ома для участка цепи (не содержащего источника тока): сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника. Величина

называется электрической проводимостью проводника. Сопротивление проводников зависит от его размеров и формы, а также от материала, из которого проводник изготовлен. Для однородного линейного проводника сопротивление R прямо пропорционально его длине l и обратно пропорционально площади его поперечного сечения S:

Единица удельного электрического сопротивления — ом-метр (Ом • м).

Закон Ома можно представить в дифференциальной форме. Подставив выражение для сопротивления (98.2) в закон Ома (98.1), получим

где величина, обратная удельному сопротивлению,

называется удельной электрической проводимостью вещества проводника. Ее единица — сименс на метр (См/м). Учитывая, что U/l=E — напряженность электрического поля в проводнике, I/S= j — плотность тока, формулу (98.3) можно записать в виде

.                                                              

Так как в изотропном проводнике носители тока в каждой точке движутся в направлении вектора Е, то направления j и Е совпадают. Поэтому формулу (98.4) можно записать в виде

Выражение (98.5) — закон Ома в дифференциальной форме, связывающий плотность тока в любой точке внутри проводника с напряженностью электрического поля в этой же точке. Это соотношение справедливо и для переменных полей.

Опыт показывает, что в первом приближении изменение удельного сопротивления, а значит и сопротивления, с температурой описывается линейным законом:

,

α — температурный коэффициент сопротивления, для чистых металлов (при не очень низких температурах) близкий к 1/273 К-1. Следовательно, температурная зависимость сопротивления может быть представлена в виде

.

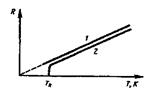
Качественный ход температурной зависимости сопротивления металла представлен на рис. 147 (кривая 1). Впоследствии было обнаружено, что сопротивление многих металлов (например, Al, Pb, Zn и др.) и их сплавов при очень низких температурах Tk (0,14—20 К), называемых критическими, характерных для каждого вещества, скачкообразно уменьшается до нуля (кривая 2), т. с. металл становится абсолютным проводником. Явление сверхпроводимости объясняется на основе квантовой теории.