Уединенный проводник – это проводник удаленный от других проводников, тел и зарядов. Его потенциал пропорционален заряду проводника. Разные проводники будучи одинаково заряжены, имеют различные потенциалы.
.
Величину
называют электроемкость уединенного проводника. Емкость уединенного проводника определяемся зарядом, сообщение которого проводнику изменяет его потенциал на единицу.
Емкость проводника зависит от его размеров и формы, но не зависит от материала, агрегатного состояния, формы и размеров полостей внутри проводника.
Единица электроемкости – фарад (Ф).
Согласно (84.5), потенциал уединенного шара радиуса R, находящегося в однородной среде с диэлектрической проницаемостью 
равен
.
Следовательно емкость шара равна
Конденсаторы
Устройства, обладающие при малых размерах и небольших относительных окружающих тел потенциалах, накапливать значительные по величине заряды, называются конденсаторами.
Конденсатор состоит из двух проводников, разделенных диэлектриком. На емкость конденсатора не должны оказывать влияние окружающие тел, поэтому проводникам придают такую форму, чтобы поле, создаваемое накапливаемыми зарядами, было сосредоточено в узком зазоре между обкладками конденсатора. Этому условию удовлетворяют: 1) две плоские пластины; 2) два коаксиальных цилиндра; 3) две концентрические сферы. Поэтому конденсаторы делятся на плоские, цилиндрические и сферические.
Под емкостью конденсатора понимается физическая величина, равная отношению заряда Q, накопленного в конденсаторе, к разности потенциалов 
между его обкладками:
Емкость плоского конденсатора равна
Энергия заряженного конденсатора.
Как всякий заряженный проводник, конденсатор обладает энергией, которая рана
,
где Q – заряд конденсатора, C – его емкость, 
- разность потенциалов между обкладками конденсатора.
Используя выражение (94.5), можно найти механическую силу, с которой пластины конденсатора притягиваются друг к другу. Для этого предположим, что расстояние x между пластинами меняется на величину dx. Тогда действующая сила совершает работу dA=Fdx вследствие уменьшения потенциальной энергии системы Fd=-dW, откуда
подставив в (94.4) выражение (94.3), получим
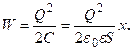
Производя дифференцирование при конкретном значении энергии найдем искомую силу
,
где знак минус указывает, что сила F является силой притяжения.
Энергия электростатического поля. Преобразуем формулу
,
Выражающую энергию плоского конденсатор посредством зарядов и потенциалов, воспользовавшись выражением для емкости плоского конденсора 
и разности потенциалов между его обкладками 
. Тогда
,
Соединения конденсаторов.
1. Параллельное соединение. У параллельно соединенных конденсаторов разность потенциалов на обкладках конденсаторов одинакова и равна 
. Если емкость отдельных конденсаторов С1, С2, …, Сn, то их заряды равны
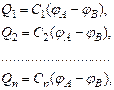
а заряд батареи конденсаторов
.
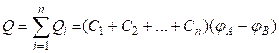Полная емкость батареи
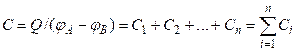
2. Последовательное соединение конденсаторов. У последовательно соединенных конденсаторов заряды всех обкладок равны по модулю, а разность потенциалов на зажимах батареи
,
где для любого из рассматриваемых конденсаторов 
. С другой стороны,
откуда
,
т.е. при последовательном соединении конденсаторов суммируются величины, обратные емкостям.
Поможем написать любую работу на аналогичную тему