Теорема Гаусса для электростатического поля в вакууме - Шпаргалка по Электростатике

Вычисление напряженности поля системы электрических зарядов с помощью принципа суперпозиции электростатических полей можно значительно упростить, используя выведенную немецким ученым К. Гауссом (1777—1855) теорему, определяющую поток вектора напряженности электрического поля сквозь произвольную замкнутую поверхность.

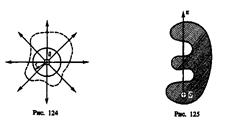
В соответствии с формулой (79.3) поток вектора напряженности сквозь сферическую поверхность радиуса г, охватывающую точечный заряд Qt находящийся в ее центре (рис. 124), равен

Этот результат справедлив для замкнутой поверхности любой формы. Действительно, если окружить сферу (рис. 124) произвольной замкнутой поверхностью, то каждая линия напряженности, пронизывающая сферу, пройдет и сквозь эту поверхность.

Нечетное число пересечений при вычислении потока в конечном счете сводится к одному пересечению, так как поток считается положительным, если линии напряженности выходят из поверхности, и отрицательным для линий; входящих в поверхность. Если замкнутая поверхность не охватывает заряда, то поток сквозь нее равен нулю, так как число линий напряженности, входящих в поверхность, равно числу линий напряженности, выходящих из нее.

Таким образом, для поверхности любой формы, если она замкнута и заключает в себя точечный заряд Q, поток вектора Е будет равен ,т. е.

Знак потока совпадает со знаком заряда Q.

Рассмотрим общий случай произвольной поверхности, окружающей n зарядов. В соответствии с принципом суперпозиции напряженность Е поля, создаваемого всеми зарядами, равна сумме напряженностей Ei полей, создаваемых каждым зарядом в отдельности: . Поэтому

Согласно (81.1), каждый из интегралов, стоящий под знаком суммы, равен . Следовательно,

Формула (81.2) выражает теорему Гаусса для электростатического воля в вакууме: поток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на .

Применение теоремы Гаусса к расчету некоторых электростатических полай в вакууме

1. Поле равномерно заряженной бесконечной плоскости. Бесконечная плоскость (рис. 126) заряжена с постоянной поверхностной плотностью  (— заряд, приходящийся на единицу поверхности). Линии напряженности перпендикулярны рассматриваемой плоскости и направлены от нее в обе стороны. В качестве замкнутой поверхности мысленно построим цилиндр, основания которого параллельны заряженной плоскости, а ось перпендикулярна ей. Так как образующие цилиндра параллельны линиям напряженности (), то поток вектора напряженности сквозь боковую поверхность цилиндра равен нулю, а полный поток сквозь цилиндр равен сумме потоков сквозь его основания, т. е. равен 2ES. Заряд заключенный внутри построенной цилиндрической поверхности, равен . Согласно теореме Гаусса (81.2), , откуда

Из формулы (82.1) вытекает, что Е не зависит от длины цилиндра, т. е. напряженность поля в любых расстояниях одинакова по модулю, иными словами, поле равномерно заряженной плоскости однородно.

2. Поле двух бесконечных параллельных разноименно заряженных плоскостей (рис. 127). Пусть плоскости заряжены равномерно разноименными зарядами с поверхностными плотностями . Поле таких плоскостей найдем как суперпозицию полей, создаваемых каждой из плоскостей в отдельности. На рисунке верхние стрелки соответствуют полю от положительно заряженной плоскости, нижние — от отрицательной плоскости. Слева и справа от плоскостей поля вычитают (линии напряженности направлены навстречу друг другу), поэтому здесь напряженность поля Е=0. В области между плоскостями  (Е+ и Е- определяются по формуле (82.1)), поэтому результирующая напряженность

Таким образом, результирующая напряженность поля в области между плоскостями описывает формулой (82.2), а вне объема, ограниченного плоскостями, равна нулю.

3. Попе равномерно заряженной сферической поверхности. Сферическая поверхность радиуса R с общим зарядом Q заряжена равномерно с поверхностной плотностью . Благодаря равномерному распределению заряда по поверхности поле, создаваемое им, обладает сферической симметрией Поэтому линии напряженности направлены радиально (рис. 128). Построим мысленно сферу радиуса r, имеющую обbщй центр с заряженной сферой. Если r>R, то внутрь поверхности попадает весь заряд Q, создающий рассматриваемое поле, и, по теореме Гаусса (81.2),  откуда

При r>R поле убывает с расстоянием r по такому же закону, как у точечного заряда. График зависимости Е от r приведен на рис. 129. Если , то замкнутая поверхность не содержит внутри зарядов, поэтому внутри равномерно заряженной сферической поверхности электростатическое поле отсутствует.

4. Потенциал электростатического поля

Тело, находящееся в потенциальном поле сил, обладает потенциальной энергией, за счет которой силами поля совершается работа. Как известно, работа консервативных сил совершается за счет убыли потенциальной энергии. Поэтому работу (83.1) сил электростатического поля можно представить как разность потенциальных энергий, которыми обладает точечный заряд Q0 в начальной и конечной точках поля заряда Q:

откуда следует, что потенциальная энергия заряда Q0 в поле заряда Q равна

Она определяется неоднозначно, а с точностью до произвольной постоянной С. Если считать, что при удалении заряда в бесконечность () потенциальная энергия обращается в нуль (U=0), то С=0 и потенциальная энергия заряда Q0 находящегося в поле заряда Q на расстоянии r от него, равна

Для одноименных зарядов Q0Q>0 и потенциальная энергия их взаимодействия (отталкивания) положительна, для разноименных зарядов Q0Q<0 и потенциальная энергия их взаимодействия (притяжения) отрицательна.

Если поле создается системой n точечных зарядов Ql, Q2, ...., Qn, то работа

электростатических сил, совершаемая над зарядом Q0, равна алгебраической сумме работ сил, обусловленных каждым из зарядов в отдельности. Поэтому потенциальная энергия U заряда Q0, находящегося в этом поле, равна сумме потенциальных энергий Ui каждого из зарядов:

Из формул (84.2) и (84.3) вытекает, что отношение U/Q0 не зависит от Q0 и являет поэтому энергетической характеристикой электростатического поля, называемой от потенциалом:

Потенциал  в какой-либо точке электростатического поля есть физическая величина, определяемая потенциальной энергией единичного положительного заряда, помещенного в эту точку.

Из формул (84.4) и (84.2) следует, что потенциал поля, создаваемого точечным зарядом Q, равен

Работа, совершаемая силами электростатического поля при перемещении заряда Q0 из точки 1 в точку 2 (см. (84.1), (84.4), (84.5)), может быть представлена как

т. е. равна произведению перемещаемого заряда на разность потенциалов в начальной и конечной точках. Разность потенциалов двух точек 1 и 2 в электростатическом поле определяется работой, совершаемой силами поля, при перемещении единичного положительного заряда из точки 1 в точку 2.

Работа сил поля при перемещении заряда Q0 из точки 1 в точку 2 может был записана также в виде

Приравняв (84.6) и (84.7), придем к выражению для разности потенциалов:

,                                   

где интегрирование можно производить вдоль любой линии, соединяющей начальную и конечную точки, так как работа сил электростатического поля не зависит от траектории перемещения.

Если перемещать заряд Q0 из произвольной точки за пределы поля, т. е. в бесконечность, где, по условию, потенциал равен нулю, то работа сил электростатического поля, согласно (84.6),  откуда

Таким образом, потенциал — физическая величина, определяемая работой по перемещению единичного положительного заряда при удалении его из данной точки поля в бесконечность. Эта работа численно равна работе, совершаемой внешними силами (против сил электростатического поля) по перемещению единичного положительного заряда из бесконечности в данную точку поля.

Из выражения (84.4) следует, что единица потенциала — вольт (В).

Вычисление разности потенциалов по напряженности поля.

1. Поле равномерно заряженной бесконечной плоскости определяется формулой: . Разность потенциалов между точками, лежащими на расстояниях x1 и x2 от плоскости, равна

2. Поле двух бесконечных параллельных разноименно заряженных плоскостей определяется формулой: . Разность потенциалов между плоскостями, расстояние между которыми равно d, равна

3. Поле заряженной сферической поверхности радиуса R с общим зарядом Q вне сферы (r>R) вычисляется по: . Разность потенциалов между двумя точками, лежащими на расстояниях r1 и r2 от центра сферы (r1>R, r2>R, r2>r1) равна

если принять r1=r и r2=∞, то потенциал поля вне сферической поверхности, согласно формуле (86.2), задается выражением

Внутри сферической поверхности потенциал всюду одинаков и равен