Расчет интерференционной картины.  

Пусть в некоторую точку А одновременно приходят две световые волны от когерентных источников света S1 и S2, световые векторы которых колеблются в одной плоскости (рис. 2.1). Пусть источники начинают излучать одновременно, начальные фазы волн равны нулю и амплитуды одинаковы. Тогда уравнения волн можно записать следующим образом:

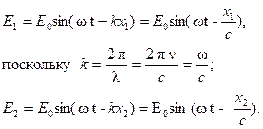
Складывая эти выражения, можно получить что результирующая величина Е в точке А будет равна:

.

Величина не зависит от времени и является амплитудой суммарного колебания в точке А. Амплитуда может принимать нулевое значение, если  а это выполняется если аргумент косинуса равен нечетному числу π/2. При этом происходит взаимное «гашение» волн и мы наблюдаем ослабление интенсивности суммарной волны, то есть интерференционный минимум. Определим положение в пространстве таких точек:

, где m = 0, 1, 2…. - любое целое число, которое называется порядком интерференции, запись  означает нечетное число. х1 и х2 – геометрические пути световых волн от источников света S1 и S2 соответственно, до произвольной точки А (рис. 2.1). Разность х2 - х1 = Δ называется геометрической разностью хода волн. Если свет распространяется в среде с показателем преломления n, необходимо рассматривать оптический путь волн l = xn. Если световые волны проходят в разных средах, их оптические пути будут l1=x1n1 и l2=x2n2 и оптическая разность хода Δ = l2 - l1. Таким образом, если в произвольной точке пространства оптическая разность хода накладываемых волн равна нечетному числу полуволн, то в ней наблюдается минимум интерференции. Условие  есть условие интерференционного минимума.

Если  что возможно при равенстве аргумента нулю или четному числу π/2, амплитуда светового вектора для данной точки будет в любой момент времени равна 2Е0. Определим положение этих точек:

.

Если в произвольной точке пространства оптическая разность хода накладываемых волн равна четному числу полуволн или целому числу длин волн, то в ней наблюдается максимум интерференции и условие  является условием интерференционного максимума. Если между световыми волнами существует разность хода, то они также обладают разностью фаз.

Получим условия интерференционных максимумов и минимумов для разности фаз δ:

.

Если вместо Δ подставить значения Δmax и Δ min, то мы получим условия максимума и минимума интерференции для разности фаз δ max = ±2πm и δ min = ±(2m+1)π, ( m = 0,1,2…).

Если амплитудные значения светового вектора не равны друг другу, т.е. Е01 ≠ Е02, то квадрат результирующей амплитуды определяется по формуле:

Е2 = Е012 + Е022 + 2Е01Е02cos (φ2 – φ1),

где (φ2 – φ1) – разность фаз колебаний. Поскольку интенсивность света I пропорциональна квадрату амплитудного значения Е, то

.

В точках пространства, где cos (φ2 – φ1) > 0, результирующая интенсивность I > I1 + I2. Если cos (φ2 – φ1) < 0, то I < I1 + I2. Таким образом, мы наблюдаем перераспределение интенсивности и интерференционную картину.