Интерференция света в тонких пленках.   - Волновая и квантовая оптика. Лекции.

В природе мы неоднократно наблюдали радужную окраску мыльных пузырей, тонких пленок нефти и масла на поверхности воды и оксидных пленок на поверхности металлов. Эти явления обусловлены интерференцией света в тонких пленках, возникающей при наложении когерентных световых волн, отраженных от верхней и нижней поверхностей пленки.

Пусть на плоскопараллельную прозрачную пластину с показателем преломления n и толщиной d под углом i падает плоская монохроматическая волна (рис. 2.4). Рассмотрим луч 1, который, коснувшись поверхности в точке О, разделится на два когерентных луча: отраженный от верхней поверхности пленки 1’ и преломленный 1’’. Луч 1’’ пройдет пленку, частично отразится от нижней ее поверхности в точке С, дойдет до точки В и, преломившись, выйдет из пленки. Проведем прямую АВ, перпендикулярную лучам 1’ и 1’’. Путь, который оба луча пройдут от этой прямой до экрана, будет одинаковым, но от точки О до АВ путь, пройденный лучами, будет различным. Найдем эту разность хода лучей Δ. С учетом показателя преломления пластинки n: Δ = =(OC+CB)·n–OA, или, как дает математический расчет, . Известно, что в процессе отражения от оптически более плотной среды, световой луч теряет половину длины волны λ/2. Если пластинка находится в воздухе, то λ/2 теряет луч 1’ в точке О и выражение для разности хода приобретает вид:

.

Если на пути лучей поставить собирающую линзу, а в ее фокальной плоскости – экран, то лучи 1’ и 1’’соберутся в точке М. Освещенность точки экрана будет максимальной, если разность хода Δ составит целое число длин волн и минимальной, если Δ составит нечетное число полуволн.

Разберем несколько различных вариантов интерференции света в тонких пленках.

1. Полосы равного наклона. Пусть на плоскопараллельную пластинку толщиной d = const падает расходящийся пучок монохроматических лучей (т.е. пучок, в котором представлены всевозможные углы падения i ≠ const) (рис. 2.5). Выделим из всего множества лучей луч 1 с углом падения i1, который в результате отражения и преломления образует лучи 1’и 1’’, и луч 2 с углом падения i2, который в результате отражения и преломления образует лучи 2’ и 2’’. Так как пластинка плоскопараллельная, лучи 1’ и 1’’, 2’ и 2’’ будут попарно параллельны и в бесконечности образуют интерференционную картину. Если параллельно пластинке расположить линзу Л, а в ее фокальной плоскости поместить экран Э, то интерференционную картину мы будем наблюдать на экране. Лучи 1’ и 1’’ встретятся на экране в точке М1, а лучи 2’ и 2’’ – в точке М2. Положение этих точек можно найти, если построить побочные оптические оси, проходящие через центр линзы O и параллельные каждой паре лучей. На рис. 2.5 это пунктирные линии ОМ1 и ОМ2, соответственно. Необходимо заметить, что в точке М1 встретятся и проинтерферируют все одинаково ориентированные лучи, падающие под углом i1. Однако, если рассмотреть луч 3 с тем же углом падения i1, но иначе ориентированный по отношению к пластинке (см. рис. 2.5), то интерференция подобных ему лучей будет наблюдаться в другой точке экрана М3, находящейся на таком же расстоянии от центра экрана, что и точка М1. Таким образом, лучи с углом падения i1, но с разными ориентациями, образуют на экране кольцо, освещенность будет зависеть от разности хода лучей. Лучи с углом падения i2 и всевозможных ориентаций образуют на экране кольцо с тем же центром, но другого радиуса. В итоге на экране получится интерференционная картина, состоящая из концентрических светлых и темных колец, каждое из которых соответствует строго определенному углу наклона (углу падения) лучей. Поэтому данная интерференционная картина получила название полос равного наклона. Если линза и экран не параллельны пластине, то полосы равного наклона будут иметь вид эллипсов.

2. Полосы равной толщины. Пусть на клиновидную пластинку малого угла наклона α (d ≠ const) с показателем преломления n падает плоская монохроматическая волна (рис. 2.6). Из множества падающих на клин лучей рассмотрим лучи 1 и 2. Отраженный луч 1’ и луч 1’’ (и, соответственно лучи 2’ и 2’’) пересекутся вблизи поверхности клина и проинтерферируют.

Мысленно проведем через точки пересечения В1 и В2 плоскость, параллельно ей разместим собирающую линзу и за линзой сопряженно с плоскостью В1 В2 установим экран Э (рис. 2.6). Чтобы определить на экране точку М1, в которой соберутся лучи 1’ и 1’’, надо через точку В1 и центр линзы О провести побочную оптическую ось до пересечения с экраном. Аналогично построим на экране точку М2. Разности хода лучей 1’ и 1’’, 2’ и 2’’ будут отличаться из-за разных толщин клина d1 и d2. Следовательно, геометрическое место точек клина, соответствующих какой-то одинаковой толщине d определит одинаковую разность хода для всех лучей, падающих на это место. Для этих лучей на экране выполняется одинаковое условие интерференции. Таким местом в клине является полоса, например, А1А2 (рис. 2.7) и на экране картина имеет вид светлых и темных полос, которые называются полосами равной толщины. В рассмотренном случае полосы равной толщины локализованы близко над поверхностью пластинки. Мы можем увидеть их и не в лабораторных условиях, так как роль линзы в данном случае играет хрусталик, а роль экрана - сетчатка нашего глаза.

Если свет падает на клиновидную пластинку нормально (луч 1’’ перпендикулярен нижней поверхности пластины), то полосы равной толщины локализованы на верхней поверхности клина. При освещении клина снизу, т.е. при наблюдении интерференции в проходящем свете, светлые и темные полосы на экране поменяются местами. Это происходит из-за того, что в данном случае нет потери полуволны. Ширина полос будет тем больше, чем меньше угол наклона α у клина. Если на клин падает белый свет, то интерференционные максимумы будут всех цветов спектра (как, например, радужная окраска мыльных пузырей).

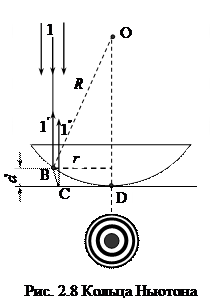3. Частным случаем полос равной толщины являются кольца Ньютона. Их можно наблюдать с помощью оптической установки, схематически изображенной на рис. 2.8. Плосковыпуклая линза большого радиуса кривизны лежит на плоской пластинке так, что между ними образуется воздушный клин переменной толщины d. Параллельный пучок света падает нормально на плоскую поверхность линзы и частично отражается от верхней (луч 1’) и нижней (луч 1’’) поверхностей воздушного клина. Лучи 1’ и 1’’ когерентные и имеют разность хода ∆ = 2d-λ/2. Такую же разность хода (а, значит, и одинаковое условие интерференции) будут иметь лучи, падающие на клин в местах одинаковой толщины d, а одинаковую толщину клин имеет по окружности. Поэтому интерференционная картина будет состоять из светлых и темных колец, называемых кольцами Ньютона. В центре картины находится темное пятно, которое обусловлено наложением лучей 1’ и 1’’ в точке D, где d = 0, а разность хода ∆ = λ/2, что соответствует условию минимума. От точки D к краям линзы толщина клина неравномерно растет, поэтому ширина и интенсивность колец убывает по мере удаления их от центрального пятна. При наблюдении колец Ньютона в проходящем свете из-за отсутствия потери полуволны в центре картины будет наблюдаться светлое пятно, затем первое темное кольцо и так далее. Максимумы в проходящем свете соответствуют минимумам в отраженном. При наклонном падении света на линзу вместо колец на интерференционной картине получаются эллипсы. Если свет будет не монохроматическим, а белым, светлые кольца приобретают радужную окраску.