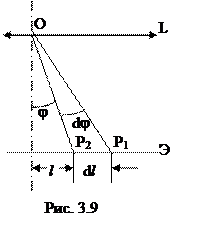Дисперсия и разрешающая сила спектрального прибора.  

Основными характеристиками любого спектрального прибора, в том числе и дифракционной решетки, являются его дисперсия и разрешающая сила. От их величин зависит способность прибора пространственно разделить лучи разных длин волн. Линейная дисперсия D определяется как отношение , где dl - расстояние между спектральными линиями, а dλ – разность длин волн этих линий. Определение справедливо также для разности частот линий dν. Угловая дисперсия , где dφ – разность углов между лучами, отличающимися на dλ или dν соответственно. На рис. 3.9 показаны два луча, идущие под углами φ и φ + dφ, и имеющие длины волн λ и λ + dλ, соответственно.

Для определения угловой дисперсии дифракционной решетки продифференцируем условие главного максимума dsinφ = = mλ. Мы получим

dcosφ dφ = mdλ,

откуда следует . При малых углах cosφ≈1 и Q ≈ ≈m/d, т.е. чем выше порядок спектра и меньше период решетки, тем больше угловая дисперсия. Она не зависит от числа щелей в решетке и характеризует степень растянутости спектра в области данной длины волны.

Разрешающая сила спектрального прибора R показывает, какие близкие спектральные линии λ1 и λ2 с разностью длин dλ = λ2 - λ1 можно визуально разделить в спектре. , где λ – средняя длина волны разрещаемых линий λ1 и λ2. На рис. 3.10 пунктиром представлены две близкие спектральные линии, а сплошной кривой показаны наблюдаемые результирующие интенсивности. В случае а) обе линии воспринимаются как одна, в случае б) линии воспринимаются раздельно. Это происходит потому, что возможность визуального разделения линий зависит также от их ширины. Согласно критерию, предложенному английским физиком Д.Рэлеем, спектральные линии считаются разрешенными, если максимум одной из них совпадает с минимумом другой (рис. 3.10 б).

Разрешающая сила дифракционной решетки R пропорциональна числу щелей N и порядку спектра m, т.е. R = Nm. Приравняв друг другу два выражения для разрешающей силы, мы получим условие разрешимости линий . Если , то спектральные линии разрешаются, если , линии не разрешаются.