Чтобы выяснить роль ширины щели S, рассмотрим теперь на примере опыта Юнга другой крайний случай: излучение монохроматическое, щель не узкая.
 Интерференционную картину на экране Э
(рис. 4.7)
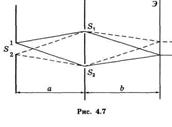
Интерференционную картину на экране Э
(рис. 4.7)
можно представить как наложение интерференционных картин от бесконечно узких щелей, на которые мысленно разобьем щель S.
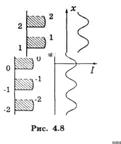
Пусть рис. 4.8. положение максимумов на экране Э от узкой щели взятой около
- верхнего края щели S ( точки 1) - отмечено сплошными отрезками
- нижнего края щели S(точки 2) — будут смещены вверх- они отмечены пунктирными отрезками.
- Интервалы между этими максимумами заполнены максимумами от промежуточных узких щелей, расположенных между краями 1 и 2.
При расширении щели S расстояния между максимумами от ее крайних элементов будут увеличиваться, т. е. интервалы между соседними максимумами от одного края щели будут постепенно заполняться максимумами от остальных элементов щели.
Будем считать, что в схеме (рис. 4.7) расстояния а = b.
Тогда
при ширине щели s, равной ширине интерференционной полосы![]() , интервал между соседними максимумами от края 1 будет целиком заполнен максимумами от остальных элементов щели, и интерференционные полосы исчезнут.
, интервал между соседними максимумами от края 1 будет целиком заполнен максимумами от остальных элементов щели, и интерференционные полосы исчезнут.
При расширении щели S интерференционная картина постепенно размывается и при некоторой ширине щели практически исчезает.
Интерференционная картина исчезает вследствие того, что вторичные источники — щели S1 и S2 (рис. 4.7) становятся некогерентными. Сказанное позволяет говорить о ширине когерентности падающей на щели S1 и S2 световой волны — ширине![]() , на которой отдельные участки волны в достаточной степени когерентны между собой.
, на которой отдельные участки волны в достаточной степени когерентны между собой.
Под шириной![]() имеется в виду характерное для данной установки расстояние между точками поверхности, перпендикулярной направлению распространения волны.
имеется в виду характерное для данной установки расстояние между точками поверхности, перпендикулярной направлению распространения волны.
Найдем формулу для вычисления ![]() .
.
В рассматриваемой схеме опыта Юнга
- запишем условие, при котором щели S1 и S2 становятся некогерентными источниками:
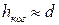 , где d — расстояние между щелями.
, где d — расстояние между щелями. - Интерференционная картина исчезает, когда ширина щели
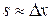 .
. - Ширина же полосы
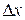 , согласно ( ), равна
, согласно ( ), равна 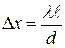
Из этих трex равенств получим:
![]()
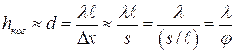 ,
,
Где φ – угловая ширина щели S относительно диафрагмы с двумя щелями.
Ширина когерентности: 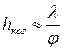
Это значит, что ширина когерентности
- пропорциональна длине волны света
- обратно пропорциональна угловой ширине источника относительно интересующего нас места (в опыте Юнга — относительно места расположения двух щелей).
Если в качестве источника использовать непосредственно Солнце (его угловой размер ф « 0,01 рад и к « 0,5 мкм), то ширина когерентности, согласно (4.12), Лког к 0,05 мм. Для получения интерференционной картины от двух щелей с помощью такого излучения расстояние между двумя щелями должно быть меньше 0,05 мм, что сделать практически невозможно.
Различают пространственную и временную когерентность.
Волновое число связано с частотой соотношением ![]() .
.
Поэтому разбросу частот ![]() соответствует разброс значений k,
соответствует разброс значений k,
- временная когерентность обусловлена разбросом значений k,
- пространственная когерентность связана с разбросом направлений вектора
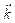 .
.
Поможем написать любую работу на аналогичную тему

