Явление интерференции состоит в отсутствии суммирования интенсивностей световых волн при их наложении, т.е. во взаимном усилении этих волн в одних точках пространства и ослаблении в других.
Необходимым условием интерференции волн является их когерентность.
Этому условию удовлетворяют
- монохроматические волны одинаковой частоты.
- Из-за поперечности электромагнитных волн этого условия недостаточно для получения интерференционной картины. Необходимо, чтобы колебания векторов
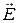 электромагнитных полей интерферирующих волн совершались вдоль одного и того же или близких направлений.
электромагнитных полей интерферирующих волн совершались вдоль одного и того же или близких направлений.
Рассмотрим две волны одинаковой частоты, которые, накладываясь друг на друга, возбуждают в некоторой точке пространства колебания одинакового направления
![]()
Амплитуда результирующего колебания в данной точке
![]() где
где ![]() .
.
Если разность фаз ![]() возбуждаемых волнами колебаний остается постоянной во времени, волны
называются когерентными.
возбуждаемых волнами колебаний остается постоянной во времени, волны
называются когерентными.
В случае некогерентных волн ![]() непрерывно меняется, принимая с равной вероятностью любые значения, поэтому среднее за период значения
непрерывно меняется, принимая с равной вероятностью любые значения, поэтому среднее за период значения ![]() равно нулю и
равно нулю и
![]() -
-
интенсивность, наблюдаемая при наложении некогерентных волн, равна сумме интенсивностей, создаваемых каждой волной в отдельности: ![]() .
.
В случае когерентных волн ![]() имеет постоянное во времени, но свое для каждой точки пространства, значение, и
имеет постоянное во времени, но свое для каждой точки пространства, значение, и
![]() .
.
- в точках пространства, где
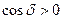
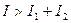 ,
, - в точках , где
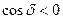
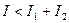 .
.
Таким образом, при наложении когерентных световых волн происходит перераспределение светового потока в пространстве, в результате чего в одних местах возникают максимумы, а в других – минимумы интенсивности. Это явление называется интерференцией волн.
Особенно отчетливо (контрастно) интерференция происходит, когда ![]() (интенсивности обеих волн одинаковы), то
(интенсивности обеих волн одинаковы), то
- в максимумах ![]() , а в минимумах
, а в минимумах ![]() .
.
Для некогерентных волн в этом случае интенсивность равна ![]() .
.
Из повседневного опыта известно: при наложении света от двух независимых источников (двух ламп накаливания) никогда не удается наблюдать явлении интерференции. Увеличение числа горящих ламп всегда приводит к возрастанию освещенности во всех точках комнаты. Применение светофильтров для «монохроматизации » излучения не приводит к появлению интерференции. Таким образом, волны, излучаемые независимыми источниками света, всегда не когерентны.
Причины указанной закономерности заключены в самом механизме испускания света атомами. Атомы обычных источников света (лампы накаливания, газоразрядные, электрические дуги ), основанных на явлении спонтанного (самопроизвольного) излучения, излучают независимо друг от друга.
Естественные источники не дают когерентного света. Это связано с тем, что излучение светящегося тела слагается из волн, испускаемых многими атомами. Излучение производится цугами (цуг – прерывистое излучение света атомами в виде отдельных кратковременных импульсов, характерно для любого источника света независимо от специфических особенностей тех процессов, которые происходят в источнике и вызывают возбуждение его атомов. Каждый цуг имеет ограниченную протяженность в пространстве, связанную с конечной длительностью его излучения) длиной до 3 м, причем фаза одного цуга никак не связана с фазой следующего.
Тем не менее , когерентные волны можно получить даже от обычных источников.
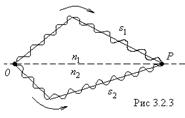 Общий принцип получения когерентных волн :
разделив волну, излучаемую одним источником, на две части (рис.3.2.3) и затем заставить эти волны пройти разные оптические пути, а потом наложить друг на друга, наблюдается интерференция.
Общий принцип получения когерентных волн :
разделив волну, излучаемую одним источником, на две части (рис.3.2.3) и затем заставить эти волны пройти разные оптические пути, а потом наложить друг на друга, наблюдается интерференция.
Разность оптических путей, проходимых волнами, не должна быть очень большой, чтобы складываемые колебания принадлежали одному цугу волн.
Пусть разделение волн происходит в точке Р.
До точки Р
- первая волна проходит в среде с показателем преломления
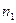 путь
путь 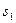 ,
, - вторая волна – в среде с показателем преломления
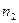 путь
путь 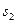 .
. - Если в точке О фаза колебаний равна
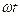 , то первая волна возбудит в точке Р колебание
, то первая волна возбудит в точке Р колебание 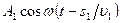 ,
, - а вторая волна – колебание
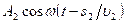 , где
, где 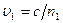 ,
, 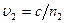 - фазовые скорости волн.
- фазовые скорости волн.
Разность фаз возбуждаемых в точке Р колебаний , равна
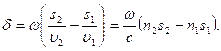
Заменив ![]() , где
, где ![]() - длина волны в вакууме,
- длина волны в вакууме,
имеем ![]() , где
, где ![]() - оптическая разность хода.
- оптическая разность хода.
Если оптическая разность хода равна
- целому числу длин волн в вакууме,
![]() (т = 0,1,2….) - условие максимума интерференции, (3.2.1)
(т = 0,1,2….) - условие максимума интерференции, (3.2.1)
(m – порядок интерференции), то разность фаз ![]() будет кратна 2π
, и колебания, возбуждаемые в точке Р обеими волнами , будут происходить в одной фазе.
будет кратна 2π
, и колебания, возбуждаемые в точке Р обеими волнами , будут происходить в одной фазе.
- полуцелому числу длин волн в вакууме,
![]() (т = 0,1,2….), - условие минимума интерференции (3.2.2)
(т = 0,1,2….), - условие минимума интерференции (3.2.2)
то ![]() , и колебания в точке Р будут в противофазе.
, и колебания в точке Р будут в противофазе.
1.  интерференция цилиндрических волн.
интерференция цилиндрических волн.
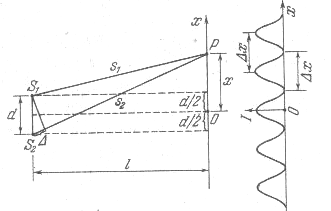
Рассмотрим две цилиндрические когерентные световые волны, исходящие из источников ![]() и
и ![]() , имеющих вид параллельных тонких светящихся нитей (рис.3.2.4).
, имеющих вид параллельных тонких светящихся нитей (рис.3.2.4).
Область, в которой эти волны перекрываются, называется полем интерференции. Во всей этой области наблюдается чередование максимумов и минимумов интерференции.
Если в поле интерференции внести экран, на нем будет видна интерференционная картина, имеющая вид чередующихся темных и светлых полос.
Вычислим ширину этих полос, если экран параллелен плоскости, проходящей через источники ![]() и
и ![]() .
.
- Положение точки на экране будем характеризовать координатой х, отсчитываемой в направлении, параллельном прямой
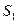
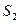 ,
, - начало отсчета выберем в точке О, относительно которой
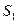 и
и 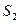 расположены симметрично.
расположены симметрично. - На рис.3.2.4
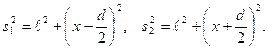
Тогда ![]()
- Для получения различимой интерференционной картины расстояние между источниками d должно быть значительно меньше расстояния до экрана
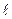 . (d<<
. (d<< 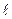 ).
). - Расстояние х, в пределах которого образуются интерференционные полосы, также много меньше
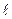 (х <<
(х << 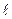 ).).
).).
Тогда ![]() , и
, и ![]() .
.
Умножив ![]() на показатель преломления среды п,
на показатель преломления среды п,
получим оптическую разность хода
![]() . (3.2.3)
. (3.2.3)
Подставив (3.2.3) в (3.2.1) и (3.2.2), получаем координаты максимумов и минимумов на экране:
![]()
где ![]() - длина волны в среде.
- длина волны в среде.
Расстояние между двумя соседними максимумами называется расстоянием между интерференционными полосами, а расстояние между двумя соседними минимумами – шириной интерференционной полосы. Эти расстояния имеют одинаковые значения
![]() . (3.2.4)
. (3.2.4)
Согласно (3.2.4),
- расстояние между полосами растет с уменьшением расстояния между источниками d.
- При d , сравнимом с
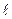 , расстояние между полосами было бы того же порядка, что и
, расстояние между полосами было бы того же порядка, что и 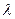 . В этом случае отдельные полосы были бы совершенно неразличимы.
. В этом случае отдельные полосы были бы совершенно неразличимы. - Чтобы интерференционная картина была отчетливой, необходимо, чтобы
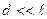 .
.
Если интенсивность интерферирующих волн одинакова, ![]() , то результирующая интенсивность в точках с разностью фаз
, то результирующая интенсивность в точках с разностью фаз ![]() равна
равна
![]() .
.
Т.к. ![]() , то согласно (3.2.3),
, то согласно (3.2.3), ![]() растет пропорционально х.
растет пропорционально х.
Следовательно, интенсивность меняется вдоль экрана по закону квадрата косинуса.
Ширина интерференционных полос и расстояние между ними зависят от длины волны ![]() .
.
- Только в центре картины, при х=0, совпадают максимумы всех длин волн.
- По мере удаления от центра максимумы разных цветов смещаются друг относительно друга все больше и больше. Интерференционная картина смазывается.
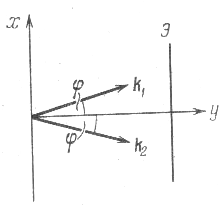 2. Рассмотрим интерференцию двух плоских волн одинаковых амплитуд. (рис.3.2.5)
2. Рассмотрим интерференцию двух плоских волн одинаковых амплитуд. (рис.3.2.5)
Направления распространения этих волн образуют угол 2φ.
Направления колебаний светового вектора будем считать перпендикулярными к плоскости рисунка. Волновые векторы ![]() и
и ![]() лежат в плоскости рисунка и равны по модулю
лежат в плоскости рисунка и равны по модулю ![]()
Уравнения этих волн
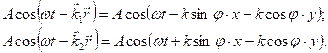
Результирующее колебание в точке с координатами х, у
![]()
Из этого выражения следует, что
- в точках, где
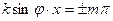 (т= 0,1,2,…), амплитуда колебаний равна 2А;
(т= 0,1,2,…), амплитуда колебаний равна 2А; - в точках, где
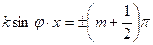 (т= 0,1,2,…), амплитуда колебаний равна нулю.
(т= 0,1,2,…), амплитуда колебаний равна нулю.
Где бы ни был экран Э, перпендикулярный оси У, на нем будет наблюдаться система чередующихся светлых и темных полос, параллельных оси Z. Координаты максимумов интенсивности
![]()
От положения экрана ( от у) зависит лишь фаза колебаний.
Поможем написать любую работу на аналогичную тему

