Проникновение световых волн в область геометрической тени можно объяснить с помощью принципа Гюйгенса (геометрический принцип). Однако этот принцип не дает сведений об амплитуде, а значит, и об интенсивности волн, распространяющихся в различных направлениях.
Френель дополнил принцип (вложил в принцип Гюйгенса физический смысл) Гюйгенса представлением об интерференции вторичных волн. Учет амплитуд и фаз вторичных волн позволяет найти амплитуду результирующей волны в любой точке пространства. Развитый таким образом принцип Гюйгенса получил название принципа Гюйгенса- Френеля.
Френель разработал следующие основные положения, являющиеся дальнейшим развитием теории Гюйгенса.
1) при распределении волн, возбуждаемых источником S0, источник S0 можно заменить системой фиктивных (виртуальных) источников и возбуждаемых ими вторичных волн. В качестве этих источников можно выбрать малые участки любой замкнутой поверхности S, охватывающей S0.
2) Вторичные источники, эквивалентные одному и тому же источнику S0, когерентны между собой, следовательно, в любой точке вне вспомогательной замкнутой поверхности S волны, реально распространяющиеся от источника S0, являющегося результатом интерференции всех вторичных волн.
3) Для поверхности S, совпадающей с волновой поверхностью, мощности вторичного излучения равных по площади участков одинаковы. Каждый вторичный источник излучает свет преимущественно в направлении внешней нормали ![]() к волновой поверхности в этой точке – амплитуда вторичных волн в направлении, составляющем с
к волновой поверхности в этой точке – амплитуда вторичных волн в направлении, составляющем с ![]() угол a тем меньше, чем больше a , и равна нулю при
угол a тем меньше, чем больше a , и равна нулю при ![]() . Френель исключил возможность возникновения «обратных» вторичных волн, распространяющихся от вторичных источников внутрь области, ограниченной поверхностью S.
. Френель исключил возможность возникновения «обратных» вторичных волн, распространяющихся от вторичных источников внутрь области, ограниченной поверхностью S.
4) В том случае, когда часть поверхности S прикрыта непрозрачными экранами, вторичные волны излучаются только открытыми участками поверхности S. Излучение этих участков не зависит от материала, формы и размеров экранов, т.е. осуществляется так, как если бы экранов не было совсем.
Исходя из принципа Гюйгенса – Френеля, можно получить закон прямолинейного распространения света в свободной от препятствий однородной среде.
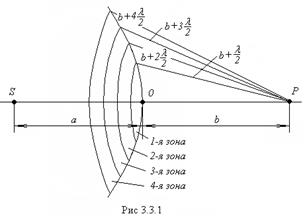 |
Пусть:
S – точечный источник света,
Р – произвольная точка, в которой нужно найти амплитуду колебаний.
Построим:
сферическую волновую поверхность радиуса а,
наименьшее расстояние от поверхности до точки Р равно b,
a+b>>l (l – длина волны света).
Амплитуда А зависит от результата интерференции вторичных волн, излучаемых всеми участками dS волновой поверхности.
Для решения этой задачи Френель предложил разбить волновую поверхность на зоны – метод зон Франеля.
- Границей первой зоны служат точки поверхности, находящиеся на расстоянии b + l/2 от точки Р.
- Точки сферы, находящиеся на расстояниях b + 2l/2 от точки Р образуют границы второй зоны Френеля и так далее.
- Расстояние внешнего края т-ной зоны до точки Р равно (рис.3.3.1)
![]()
- Колебания, возбуждаемые в точке Р двумя соседними зонами, противоположны по фазе, так как разность хода между ними l/2.
Поэтому при наложении эти колебания ослабляют друг друга:
А= А1 – А2 + А3 – А4 + … . (3.3.1)
А1, А2 – колебания, возбуждаемые каждой зоной порознь.
Величина Ai зависит
- от площади si i – той зоны
- и угла ![]() между внешней нормалью к поверхности зоны в какой – либо ее точке и прямой, направленной из этой точки в точку Р.
между внешней нормалью к поверхности зоны в какой – либо ее точке и прямой, направленной из этой точки в точку Р.
Можно показать, что площади всех зон Франеля одинаковы:
![]() .
.
Радиус внешней границы т-ной зоны равен
![]()
- радиусы зон возрастают пропорционально ![]() .
.
В случае плоской волны ![]() и
и ![]() .
.
С увеличением номера зоны возрастает угол ![]() , и следовательно уменьшается интенсивность излучения зоны в направлении точки Р, т.е. уменьшается амплитуда
, и следовательно уменьшается интенсивность излучения зоны в направлении точки Р, т.е. уменьшается амплитуда ![]() , т.е. А1> А2>…> Аi>…
, т.е. А1> А2>…> Аi>…
Можно считать, что в пределах малых изменений i зависимость Ai от i является линейной,
![]() ,
,
тогда
![]() (3.3.2)
(3.3.2)
Подставив (3.3.2) в (3.3.1), имеем
![]()
- результирующее действие в точке Р полностью открытого фронта световых волн, возбуждаемых источником S, равно половине действия одной только центральной зоны Френеля, радиус которой мал, следовательно, с достаточно большой точностью можно считать, что в свободном пространстве свет от источника S в точку Р распространяется прямолинейно.
метод графического сложения амплитуд
Теперь решим задачу о распространении света от источника ![]() к точке
к точке ![]() методом графического сложения амплитуд.
методом графического сложения амплитуд.
Разобьем волновую поверхность на кольцевые зоны, аналогичные зонам Френеля, но гораздо меньшие по ширине (разность хода от краев зоны до точки ![]() составляет одинаковую для всех зон малую долю
составляет одинаковую для всех зон малую долю ![]() ).
).
Изобразим колебание, создаваемое в точке ![]() каждой из зон:
каждой из зон:
- в виде вектора, длина которого равна амплитуде колебания,
 - а угол, образуемый вектором с направлением, принятым за начало отсчета, дает начальную фазу колебания.
- а угол, образуемый вектором с направлением, принятым за начало отсчета, дает начальную фазу колебания.
Амплитуда колебаний, создаваемых такими зонами в точке ![]() , медленно убывает при переходе от зоны к зоне.
, медленно убывает при переходе от зоны к зоне.
Каждое следующее колебание отстает от предыдущего по фазе на одну и ту же величину. Следовательно, векторная диаграмма, получающаяся при сложении колебаний, возбуждаемых отдельными зонами, имеет вид, показанный на рис.3.3.2.
Если бы амплитуды, создаваемые отдельными зонами, были одинаковыми, конец последнего из изображенных на рис. 3.3.2 векторов совпал бы с началом первого вектора.
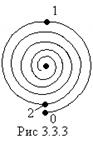 В действительности значение амплитуды, хотя и очень слабо, но убывает, вследствие чего векторы образуют не замкнутую фигуру, а ломаную спиралевидную линию.
В действительности значение амплитуды, хотя и очень слабо, но убывает, вследствие чего векторы образуют не замкнутую фигуру, а ломаную спиралевидную линию.
В пределе при стремлении ширины кольцевых зон к нулю (количество их будет при этом неограниченно возрастать) векторная диаграмма примет вид спирали, закручивающейся к точке ![]() (рис. 3.3.3).
(рис. 3.3.3).
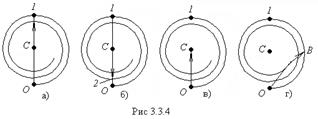 |
Фазы колебаний в точках 0 и 1 отличаются на
Следовательно,
- участок спирали 0 - 1 соответствует первой зоне Френеля.
Вектор, проведенный из точки 0 в точку 1 (рис. 3.3.4, а), изображает колебание, возбуждаемое в точке ![]() этой зоны.
этой зоны.
- Аналогично, вектор, проведенный из точки 1 в точку 2 (рис. 3.3.4, б), изображает колебание, возбуждаемое второй зоной Френеля.
- Колебания от первой и второй зон находятся в противофазе; в соответствии с этим векторы 01 и 12 направлены в противоположные стороны.
- Колебание, возбуждаемое в точке
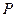 всей волновой поверхностью, изображается вектором
всей волновой поверхностью, изображается вектором 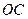 (рис. 3.3.4, в).
(рис. 3.3.4, в).
Из рисунка видно, что амплитуда в этом случае равна половине амплитуды, создаваемой первой зоной. Этот результат мы получили ранее алгебраически.
- Заметим, что колебание, возбуждаемое внутренней половиной первой зоны Френеля, изображается вектором
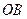 (рис. 3.3.4, г).
(рис. 3.3.4, г).
Таким образом,
- действие внутренней половины первой зоны Френеля не эквивалентно половине действия первой зоны.
- Вектор ![]() в
в ![]() раз больше вектора
раз больше вектора ![]() .
.
Следовательно, интенсивность света, создаваемая внутренней половиной первой зоны Френеля, в два раза превышает интенсивность, создаваемую всей волновой поверхностью.
Колебания от четных и нечетных зон Френеля находятся в противофазе и, следовательно, взаимно ослабляют друг друга.
 Если поставить на пути световой волны пластинку, которая перекрывала бы все четные или нечетные зоны, то интенсивность света в точке
Если поставить на пути световой волны пластинку, которая перекрывала бы все четные или нечетные зоны, то интенсивность света в точке ![]() резко возрастает. Такая пластинка, называемая зонной, действует подобно собирающей линзе.
резко возрастает. Такая пластинка, называемая зонной, действует подобно собирающей линзе.
На рис. 3.3.5 изображена пластинка, перекрывающая четные зоны.
Еще большего эффекта можно достичь, не перекрывая четные (или нечетные) зоны, а изменяя фазу их колебаний на ![]() . Это можно осуществить с помощью прозрачной пластинки, толщина которой в местах, соответствующих четным или нечетным зонам, отличается на надлежащим образом подобранную величину. Такая пластинка называется фазовой зонной пластинкой. По сравнению с перекрывающей зоны амплитудной зонной пластинкой фазовая дает дополнительное увеличение амплитуды в два раза, а интенсивности света - в четыре раза.
. Это можно осуществить с помощью прозрачной пластинки, толщина которой в местах, соответствующих четным или нечетным зонам, отличается на надлежащим образом подобранную величину. Такая пластинка называется фазовой зонной пластинкой. По сравнению с перекрывающей зоны амплитудной зонной пластинкой фазовая дает дополнительное увеличение амплитуды в два раза, а интенсивности света - в четыре раза.
Поможем написать любую работу на аналогичную тему

