Интерференция света в тонких пленках - Лекции по Оптике.

• При отражении от плоскопараллельной пластинки.

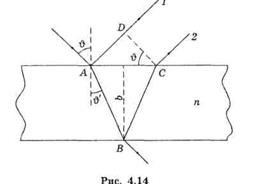
 Пусть на прозрачную плоскопараллельную пластинку падает плоская монохроматическая световая волна, направление распространения которой показано падающим лучом на рис. 4.14. В результате отражений от обеих поверхностей пластинки исходная волна расщепится на две, что и показано лучами 1 и 2.

Амплитуды этих волн мало отличаются друг от друга — это важно для получения достаточно контрастной интерференции.

Кроме этих двух отраженных волн (I и 2), возникает еще многократное отражение. Однако их вклад практически пренебрежимо мал.

Оптическую разность хода волн 1 и 2 определим, согласно рис. 4.14, как

,

где п — показатель преломления вещества пластинки.

Кроме того, видно, что  и ,

Где b-толщина пластинки.

В результате подстановки этих выражений в (   ) получим

Следует также учесть, что при отражении от верхней поверхности пластинки (от среды, оптически более плотной) в соответствии с происходит скачок фазы на π у отраженной волны, т. е., как говорят, «потеря» полуволны  (±).

 Учитывая еще,, получим

(здесь можно было написать и   +, но это не существенно).

Если отраженные волны 1 и 2 когерентны между собой (а мы об этом позаботимся), то максимумы отражения будут наблюдаться при условии

где т — целое число (порядок интерференции).

Меняя угол падения 9, мы будем наблюдать последовательную смену максимумов и минимумов отражения. (Заметим, что при минимуме отражения наблюдается максимум проходящего через пластинку света, и наоборот.)

 Если бы обе отраженные волны были некогерентными, то такого явления мы не наблюдали бы: по мере увеличения угла падения интенсивность отраженного света монотонно уменьшалась бы.

Выясним условия, при которых отраженные волны будут когерентными и смогут интерферировать.

Выделим в падающей волне некоторую область когерентности (слегка затемнена на рисунке).

• 
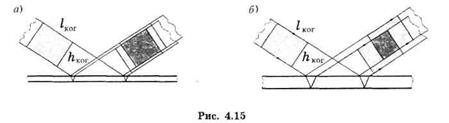
  После расщепления падающей волны расщепится и выделенная область когерентности: в отраженных волнах эти области когерентности сместятся друг относительно друга (рис. 4.15 а).
• Если при этом они перекрываются (более темный участок) – интерференция будет наблюдаться: тем более отчетливо, чем больше степень перекрытия.

Для пластинки с большей толщиной (рис. 4.15, б):  область перекрытия когерентных участков уменьшается и интерференция будет наблюдаться все менее отчетливо. Начиная с некоторой толщины пластинки интерференция исчезнет совсем.

Интерференция будут наблюдаться при условии: если смещение расчлененных частей области когерентности происходящее :

1. вдоль распространения волны – не должно превосходить длину когерентности;
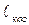2. поперек распространения волны - не должно превосходить ширину когерентности .

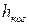Для лучшей видимости надо взять половину значений и .

Необходимо, чтобы оптическая разность хода , тогда

Для оценки ширины пластинки b будем считать:

-  (что обычно и бывает);

-  пренебрежем.

Тогда получим

,

Удвоенная пластинка не должна быть более половины длины когерентности используемого излучения.

Поперечный сдвиг частей области когерентности не должен превосходить половины ширины когерентности .

Это сдвиг (рис. 4.14) равен отрезку DC . Значит необходимо, чтобы

Из рис. 4.14 следует

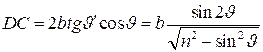
Смещение существенно зависит от угла падения :

- чем меньше угол падения, тем меньше смещение DC, тем меньше может быть . И основную роль в этом случае будет играть длина когерентности.

- При  = 0 смещение происходит только вдоль распространения волн, поперек — оно равно нулю, и ширина когерентности и становится практически не существенной.

Итак, мы выяснили, что при падении плоской световой волны на плоскопараллельную тонкую пластинку интенсивность отраженного света зависит от угла падения. Изменяя этот угол, мы будем наблюдать чередование максимумов и минимумов отраженного света. Это можно использовать для получения интерференционной картины в виде привычной системы полос.

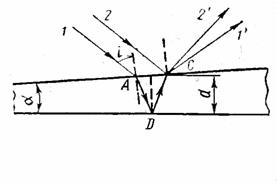•  Клин. (рис.3.2.13).

 Рассмотрим интерференцию в больших пленках, толщина которых неодинакова в разных местах.

Пусть пленка имеет форму клина с углом a между боковыми гранями.

На клин падает плоская волна, направление которой совпадает с лучами 1 и 2.

 Направление распространения интерферирующих волн, которые возникают в результате отражения от верхней и нижней границ, соответствуют 1/ и 2/. Каждому значению d соответствует одинаковая разность хода D, следовательно, одинаковые и результаты интерференции.

Поэтому в отраженном свете наблюдаются полосы равной толщины.

Верхняя и нижняя грани клина не параллельны между собой, поэтому отраженные лучи 1/ и 2/ имеют разные направления и пересекаются только в точках верхней поверхности клина.

Полосы равной толщины локализованы на поверхности клина.

Полосы равной толщины можно наблюдать в тонкой клиновидной прослойке воздуха между поверхностями двух прозрачных пластинок.  Если направление наблюдения близко к нормальному, то оптическая разность хода лучей, отраженных от поверхностей клина в месте, где ширина зазора равна b, определяется как

.

Там, где 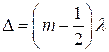, m=1,2,…- возникают минимумы.

Т.е. темные полосы возникают в тех местах, где толщина зазора .

Переход от одной полосы к соседней (ширина полосы) соответствует изменению толщины зазора на .

Каждая полоса соответствует определенной толщине зазора.

Это используют для проверки качества оптических поверхностей  при их шлифовке, наблюдая в отраженном свете прослойку между контролируемой и эталонной поверхностями.

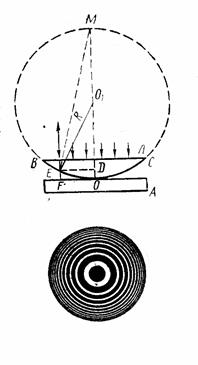•  Частным случаем полос равной толщины являются  кольца Ньютона (рис.3.2.14).

 Плосковыпуклая линза Л с большим  радиусом кривизны выпуклой поверхности обращена выпуклой стороной к плоской пластинке А и соприкасается с ней в точке О.

Параллельный пучок света падает нормально на плоскую поверхность ВС линзы и частично отражается от верхней и нижней поверхностей воздушного промежутка между линзой и пластиной.

• При наложении отраженных волн возникают интерференционные кольца равной толщины.

В центре находится темное кольцо (минимум нулевого порядка). Оно окружено системой чередующихся светлых и темных колец, ширина и интенсивность которых постепенно убывают по мере удаления от центрального пятна.

• В проходящем свете наблюдается обратная картина – центральное пятно светлое, следующее кольцо темное, и т.д.

Оптическая разность хода между лучами, отраженными от верхней и нижней поверхностей воздушного зазора на произвольном расстоянии  r=DE   от точки О, равна

показатель преломления воздуха принят равным единице,  учитывает сдвиг фаз на p при отражении света от поверхности пластины.

Из подобия прямоугольных треугольников EOD и  EDM  имеем

где так как  

Тогда  и

Подставив это выражение в условия максимумов и минимумов интерференции, получаем: радиусы т-ных светлого  и темного  колец Ньютона

• в отраженном свете:

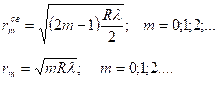
• в проходящем свете

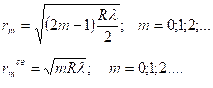
Значению m = 0 соответствует минимум темного пятна (не кольца).

Правильная форма колец Ньютона легко искажается при всяких, даже незначительных дефектах в обработке выпуклой поверхности линзы и верхней поверхности  пластины. Поэтому наблюдение колец Ньютона позволяет осуществить быстрый и весьма точный контроль качества шлифовки плоских пластин и линз, а так же близость их поверхностей к сферической форме.