Классическим примером полос равной толщины являются кольца Ньютона (1675г.). Роль тонкой пленки, от поверхностей которой отражаются когерентные волны, играет воздушный зазор между плоскопараллельной стеклянной пластинкой и соприкасающейся с ней выпуклой поверхностью плосковыпуклой линзы с большим радиусом кривизны.
При нормальном падении света интерференционная картина в отраженном свете имеет вид: в центре расположено темное пятно (min нулевого порядка), окруженное рядом концентрических светлых и темных колец убывающей ширины и интенсивности. При наклонном падении кольца превращаются в эллипсы. В белом свете возникают цветные кольца с центром в точке касания линзы. Интерференционная картина в проходящем свете будет дополнительной. Как уже отмечалось, более контрастными будут кольца в отраженном свете.
Условие наблюдения в принципиальном отношении такие же, как и в случае тонких пленок.
Оптическая разность хода между лучами, отраженными от верхней и нижней поверхностей воздушного зазора в точке с толщиной dm: 
, т.к. j1=0, nв=1.
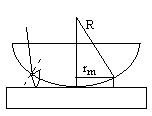
Темное пятно в центре возникает в результате того, что разность хода равна 0 и происходит лишь потеря l/2 при отражении от плоской стеклянной поверхности. Но 
, rm – радиус m-го кольца, R - радиус кривизны поверхности линзы. Для темных колец 
. Тогда 
- радиусы темных колец.
С помощью колец Ньютона, как и в опыте Юнга, можно сравнительно просто определить l.
Правильная форма колец Ньютона легко искажается при незначительных дефектах в обработке выпуклой поверхности линзы и верхней поверхности пластины. Поэтому наблюдение формы колец Ньютона позволяет осуществлять быстрый и весьма точный контроль качества шлифовки плоских пластин и линз, а так же близость поверхностей линз к сферической форме.
Поможем написать любую работу на аналогичную тему