Частным случаем полос равной толщины являются кольца Ньютона
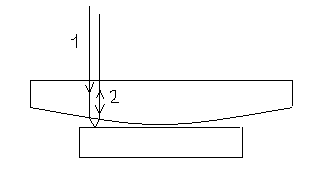Плосковыпуклая линза Л с большим радиусом кривизны выпуклой поверхности обращена выпуклой стороной к плоской пластинке А и соприкасается с ней в точке О.
Параллельный пучок света падает нормально на плоскую поверхность ВС линзы и частично отражается от верхней и нижней поверхностей воздушного промежутка между линзой и пластиной.
При наложении отраженных волн возникают интерференционные кольца равной толщины.
В центре находится темное кольцо (минимум нулевого порядка). Оно окружено системой чередующихся светлых и темных колец, ширина и интенсивность которых постепенно убывают по мере удаления от центрального пятна.
В проходящем свете наблюдается обратная картина – центральное пятно светлое, следующее кольцо темное, и т.д.
Оптическая разность хода между лучами, отраженными от верхней и нижней поверхностей воздушного зазора на произвольном расстоянии r=DE от точки О, равна
показатель преломления воздуха принят равным единице, 
учитывает сдвиг фаз на p при отражении света от поверхности пластины.
Из подобия прямоугольных треугольников EOD и EDM имеем
где 
так как 
Тогда 
и 
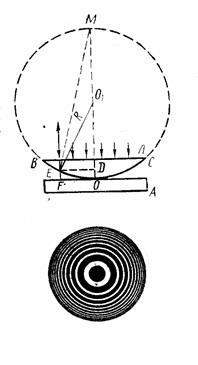Подставив это выражение в условия максимумов и минимумов интерференции, получаем: радиусы т-ных светлого 
и темного 
колец Ньютона
- в отраженном свете:
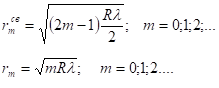
- в проходящем свете
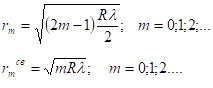
Значению m = 0 соответствует минимум темного пятна (не кольца).
Правильная форма колец Ньютона легко искажается при всяких, даже незначительных дефектах в обработке выпуклой поверхности линзы и верхней поверхности пластины. Поэтому наблюдение колец Ньютона позволяет осуществить быстрый и весьма точный контроль качества шлифовки плоских пластин и линз, а так же близость их поверхностей к сферической форме.
Поможем написать любую работу на аналогичную тему