Отражение и преломление света на границе раздела двух диэлектриков.

    Когда свет достигает границы раздела двух сред с разными оптическими свойствами, он частично проходит во вторую среду, изменяя направление в случае наклонного падения, частично отражается в первую среду. Направление отражённого и преломлённого света описывается законами геометрической оптики. Однако эти законы ни чего не говорят о поляризации и интенсивности отражённого и преломлённого света. Ответ даётся на основе электромагнитной теории света.

   Появление преломлённой и отражённой световых волн на границе раздела сред обусловлено теми же физическими причинами, что и изменение фазовой скорости волн при её распространении в неограниченной среде по сравнению со скоростью света в вакууме. С точки зрения электромагнитной теории электрическое поле падающей волны раскачивает  входящие в состав вещества заряжённые частицы, которые становятся источниками вторичных  волн. В результате интерференции этих когерентных вторичных волн формируются отражённые и преломлённые волны, направления которых и определяют максимумы интерференции.

    Задача решается  в рамках макроскопической электродинамики, т.е. с помощью уравнений Максвелла и феноменологических материальных уравнений, в которых среды рассматриваются как сплошные, а их оптические свойства задаются показателями преломления.

   При этом законы отражения и  преломления, а также выраженные формулами Френеля соотношения между амплитудами и фазами падающей, отражённой и преломлённой волн получаются как следствие граничных условий для электромагнитного поля, вытекающих из уравнений Максвелла.

   Поведение волны на границе сред полностью определяется граничными условиями для векторов поля волны которые при отсутствии свободных зарядов и токов проводимости имеют вид:

  для нормальных составляющих векторов (индексы n):)

D 2n = D1n ,

В2n = В1n ,

  для тангенциальных составляющих (индексы t)

Е2t = Е1t ,

Н2t = Н1t ,

  или

e2Е2n = e1Е1n ,

m2Н2n = m1Н1n ,

   Где e1, m1, e2, m2 – относительные диэлектрические и магнитные проницаемости соответственно первой и второй сред.

   В первой среде электромагнитное поле создаётся падающей и отражённой волной, во второй– преломлённой.

    Напряжённости электрического поля падающей, отражённой и преломлённой волн имеют вид:

Епад = Е0 пад е-i(wпад t – kпад r), …

    Записав граничные условия и учитывая, что они должны выполняться в любой момент времени для данной точки падения, получим, что это возможно при

wотр = wпрел = wпад

   Утверждение справедливо для нелазерных немощных световых пучков. Если падающая волна мощная, то возможно вторичное переизлучение на гармониках.

   Граничные условия должны выполняться в любой точке границы раздела сред. Это требование выполняется, если отражённый, преломлённый и падающий луч лежит в одной плоскости, называемой плоскостью падения. Отсюда же вытекают и законы геометрической оптики: закон отражения и преломления.

   Всякую плоскую монохроматическую световую волну можно представить в виде совокупности двух плоских монохроматических волн той же частоты, распространяющихся в одном направлении с одинаковой скоростью u, в которых векторы Е колеблются вдоль двух взаимно – перпендикулярных направлений. Если падающая волна неполяризована (естественный свет), то эти две компоненты между собой не согласованы по фазе. При этом:

   Для нахождения закономерностей отражения и преломления плоских волн на границе достаточно рассмотреть порознь плоскую волну, в которой вектор Е колеблется в плоскости падения, и плоскую волну, в которой вектор Е колеблется перпендикулярно плоскости падения. Для получения окончательного выражения для  в любой момент времени, необходимо найти суперпозицию:

.

   В дальнейшем предполагается,  что обе среды полубесконечны, т.е. неограниченно прос-тираются по обе  стороны от  границы раздела. Поэтому можно не учитывать многократного отражения  и считать, что у границы раздела сходятся только три волны: падающая, от-ражённая и преломлённая.

  Рассмотрим вначале волну, у которой Е колеблется в плоскости падения.

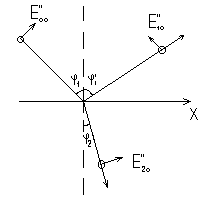
  Будем считать  численные значения векторов Е положительными, если их направления совпадают с теми, что на рисунке. Тогда

      Но  Н = nЕ ,  т.к.  m » 1

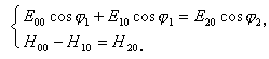
      Отсюда:

 ,

 ,

   Аналогично для проекций Е на нормаль к границе:

 ,

 .

   Соотношение (….) называют формулами Френеля.

   Амплитудные коэффициенты Френеля:

 Отражения          ,        ;

 Пропускания          ,         .

   При параллельном падении теряет смысл понятие плоскости поляризации и нет смысла говорить о  и , т.к. они становятся равноправными.

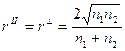
   Из формул Френеля можно найти фазовые соотношения между отражённой или преломлённой и падающей волнами.

   При обычном падении (n1 < n2) для любого угла падения j1 угол преломления j2 и все коэффициенты Френеля вещественны. Следовательно отражение и преломление не сопро-вождается изменением фазы, за исключением, может быть, изменения фазы отражённой волны на p (если соответствующий коэффициент отрицателен (при n1 < n2)).

   Для энергетического описания процессов  на границе раздела вводят понятие энергетических коэффициентов отражения R и пропускания t.

 ,

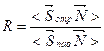      -- вектор Умове-Пойтинга,

     -- единичный вектор нормали к фронту.

Т.е. коэффициент отражения R есть отношение среднего по времени отражённого потока энергии к падающему потоку. Или , I – интенсивность света.

   В соответствии с законом сохранения энергии: Iпад = Iотр + Iпрел =>

R + t = 1 ,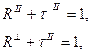                                      

   где       .

   При нормальном падении

,            t

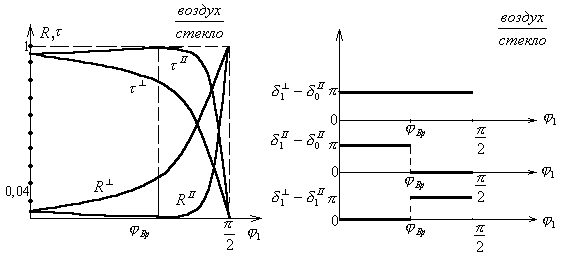
   Для границы раздела воздух-стекло при нормальном падении R = 0,4, при этом R не зависит от того, со стороны какой среды происходит падение. В оптических приборах, содержащих большое число линз и призм, потери энергии при многократном отражении могут привести к значительному ослаблению энергии света на выходе из прибора. Для уменьшения этих потерь привлекают «просветлённую оптику».

   Если падающий свет линейно поляризован с азимутом a, то отражённая и преломленная волны так же линейно поляризованы. При этом:

   Для естественного (неполяризованного) света имеет место осевая симметрия. , и говорят о суммарном коэффициенте отражения .

  Углы j1 и j2 заключены в пределах 0 £ j1, j2 £. Поэтому при любых значениях j1 и

j2 (при n1 > n2 и при n2 > n1) tII и t^ положительны, т.е. на границе раздела сред фаза пре-ломлённой волны всегда совпадает с фазой падающей волны.

   Для отражённой волны при n1 > n2 (из оптически более плотной в менее плотную).

                        j1 < j2

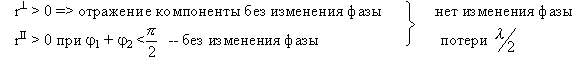
rII < 0 при j1 + j2 > -- противоположны по знаку                     

 при n1 < n2 (из менее плотной в более плотную)                        

                          j1 > j2  

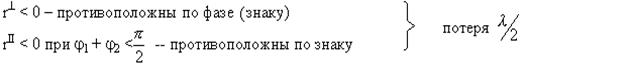
    rII > 0 при j1 + j2 > -- совпадают  я

   При малых углах падения (j1 + j2 <), т.е. когда j1 < j1Бр изменение фазы происходит при отражении от оптически более плотной среды на p (потери ).При n1 > n2 изменение фазы происходит у вектора .

   Преломлённый на границе диэлектрика неполяризованный свет (кроме случая j1= 0 и j1=) становится частично поляризованным. Степень поляризации

   Исследования показывают, что в отражённом луче преобладают колебания, перпен-дикулярные плоскости падения, в преломлённом – колебания, параллельные плоскости падения.

   Степень поляризации отражённого и преломлённого света зависит от  угла падения лучей и показателей преломления сред.

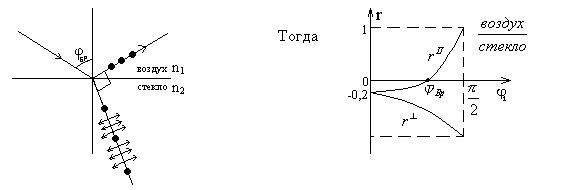
   Угол падения, при котором отражённый и преломлённый лучи взаимно перпендикулярны (расходятся под углом ), называется углом Брюстера. Т.е. сумма углов падения и преломления также равна :

   Из закона преломления можно получить: .

   Для границы раздела воздух – стекло jБр = 56°20¢.

   Шотландский физик Д.Брюстер (1781 – 1868) установил закон, согласно которому при угле падения jБр, определяемого условием , отражённый луч является плоскополяри-зованным (содержит только колебания, перпендикулярные плоскости падения), т.е.  .

   Преломлённый луч при этом поляризуется максимально, но не полностью, в плоскости падения.

   Степень поляризации преломлённого света может быть значительно повышена (многократным преломлением при условии падения света каждый раз на границу раздела под углом Блюстера). Если например, для стеклянной плоскопараллельной пластины (n = 1,33) степень поляризации преломлённого луча составляет 15% (на каждую границу 8% ), то после преломления на 8 – 10 наложенных друг на друге стеклянных пластинках вышедший из такой системы свет будет практически полностью поляризованным. Такая совокупность пластинок называется стопой. Стопа может служить для анализа поляризованного света, как при его отражении так и при его преломлении.

   Законы отражения и преломления, выведенные для плоской границы раздела сред, приблизительно верны и для искривлённой границы, если её радиус кривизны значительно больше длины волны света.