Упругая волна называется гармонической, если соответствующие ей колебания частиц среды являются гармоническими, т.е. описываются по закону синуса или косинуса. Часто гармоническую волну называют синусоидальной.
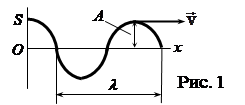На рис.1 представлена гармоническая поперечная волна, распространяющаяся со скоростью v вдоль оси x, т.е. приведена зависимость между смещением S частиц среды и расстоянием х
этих частиц от источника колебаний О для фиксированного момента времени t.
Расстояние между ближайшими частицами, колеблющимися в одинаковой фазе, называется длиной волны l. Длина волны равна тому расстоянию, на которое распространится гармоническая волна за время, равное периоду колебаний Т, т.е.
. (1)
Учитывая, что частота v = 1/T получаем
l = v / v. (2)
т.е. длина волны обратно пропорциональна частоте.
Уравнение такой волны в общем случае имеет вид
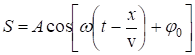, (3)
Для характеристики волн используется волновое число
, (4)
где w = 2p/T = 2pv – циклическая, (круговая) частота.
С учетом (4) получим уравнение бегущей гармонической волны
, (5)
где А – амплитуда волны, 
– фаза волны, j0 – начальная фаза.
Основываясь на формуле Эйлера (
), уравнение (5) можно записать в экспоненциальной (комплексной) форме
, (6)
где физический смысл имеет лишь действительная часть выражения (6). Такая форма представления волны существенно облегчает математический действия.
Поможем написать любую работу на аналогичную тему