Энергия бегущей волны. Вектор плотности потока энергии - Оптика. Элементы квантовой механики. Лекции.

         Упругая среда, в которой распространяется волна, обладает как кинетической энергией колебательного движения частиц, так и потенциальной энергией, обусловленной деформацией среды. Можно показать, что объемная плотность энергии для плоской бегущей гармонической волны (5)

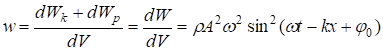                            ,         (15)

где r=dm/dV – плотность среды, т.е. периодически изменяется от 0 до rА2w2 за время p/w=Т/2.

         Среднее значение плотности энергии за промежуток времени p/w=Т/2

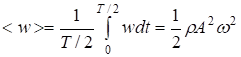                                                .                         (16)

         Для  характеристики переноса энергии вводят понятие вектора плотности потока энергии – вектор Умова.

         Выведем выражение для него.

         Если через площадку DS^, перпендикулярную к направлению распространения волны, переносится за время Dt энергия DW, то плотность потока энергии

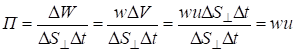                                   ,               (17)

где DV=DS^ uDt – объем элементарного цилиндра, выделенного в среде.

         Поскольку скорость переноса энергии или групповая скорость есть вектор, то и плотность потока энергии можно представить в виде вектора

                                                        , Вт/м2.                                  (18)

Этот вектор  ввел профессор Московского университета Н.А. Умов в 1874 г.

         Среднее значение его модуля называют интенсивностью волны

                                                  .                             (19)

          Для гармонической волны u=v , поэтому для такой волны в формулах (17)-(19) u можно заменить на v.