 Рассмотрим две сопряженные плоскости, перпендикулярные к оптической оси системы. Отрезок прямой
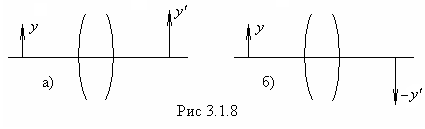
Рассмотрим две сопряженные плоскости, перпендикулярные к оптической оси системы. Отрезок прямой ![]() (рис. 3.1. 8.) лежащий в одной из этих плоскостей, будет иметь своим изображением отрезок прямой
(рис. 3.1. 8.) лежащий в одной из этих плоскостей, будет иметь своим изображением отрезок прямой ![]() , лежащий в другой плоскости. Из осевой симметрии системы вытекает, что отрезки
, лежащий в другой плоскости. Из осевой симметрии системы вытекает, что отрезки ![]() и
и ![]() должны лежать в одной, проходящей через оптическую ось, плоскости (в плоскости рисунка). При этом изображение
должны лежать в одной, проходящей через оптическую ось, плоскости (в плоскости рисунка). При этом изображение ![]() может быть обращено либо в ту же сторону, что и предмет
может быть обращено либо в ту же сторону, что и предмет ![]() (рис. 8, а), либо в противоположную сторону (см. рис. 3.1. 8, б). В первом случае изображение называется прямым, во втором - обратным. Отрезки, откладываемые от оптической оси вверх, принято считать положительными, откладываемые вниз – отрицательными.
(рис. 8, а), либо в противоположную сторону (см. рис. 3.1. 8, б). В первом случае изображение называется прямым, во втором - обратным. Отрезки, откладываемые от оптической оси вверх, принято считать положительными, откладываемые вниз – отрицательными.
Отношение линейных размеров изображения и предмета называется линейным или поперечным увеличением. Обозначив его буквой ![]() , можно написать
, можно написать
![]() .
.
Линейное увеличение - алгебраическая величина. Оно положительно, если изображение прямое (знаки ![]() и
и ![]() одинаковы), и отрицательно, если изображение обратное (знак
одинаковы), и отрицательно, если изображение обратное (знак ![]() противоположен знаку
противоположен знаку ![]() ).
).
Существуют две такие сопряженные плоскости, которые отображают друг друга с линейным увеличением ![]() . Эти плоскости называются главными. Плоскость, принадлежащая пространству предметов, именуется передней главной плоскостью системы. Ее обозначают буквой
. Эти плоскости называются главными. Плоскость, принадлежащая пространству предметов, именуется передней главной плоскостью системы. Ее обозначают буквой ![]() . Плоскость, принадлежащую пространству изображений, именуют задней главной плоскостью. Ее обозначают символом
. Плоскость, принадлежащую пространству изображений, именуют задней главной плоскостью. Ее обозначают символом ![]() . Точки пересечения главных плоскостей с оптической осью называются главными точками системы
. Точки пересечения главных плоскостей с оптической осью называются главными точками системы
(соответственно передней и задней). Их обозначают теми же символами ![]() и
и ![]() . В зависимости от устройства системы главные плоскости и точки могут находиться как вне, так и внутри системы. Может случиться, что одна из плоскостей проходит вне, а другая - внутри системы. Возможно, наконец, что обе плоскости будут лежать вне системы по одну и ту же сторону от нее.
. В зависимости от устройства системы главные плоскости и точки могут находиться как вне, так и внутри системы. Может случиться, что одна из плоскостей проходит вне, а другая - внутри системы. Возможно, наконец, что обе плоскости будут лежать вне системы по одну и ту же сторону от нее.
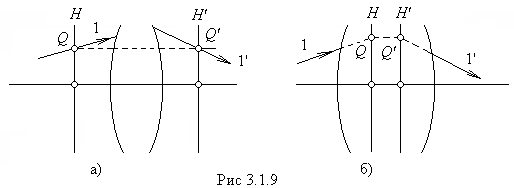 Из определения главных плоскостей вытекает, что луч 1, пересекающий (в действительности – рис. 3.1.9, а или при воображаемом продолжении
Из определения главных плоскостей вытекает, что луч 1, пересекающий (в действительности – рис. 3.1.9, а или при воображаемом продолжении
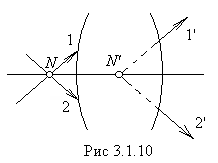 внутри системы – рис. 3.1. 9, б) переднюю главную плоскость
внутри системы – рис. 3.1. 9, б) переднюю главную плоскость ![]() в точке
в точке ![]() , имеет в качестве сопряженного луч 1', который пересекает (непосредственно или при воображаемом продолжении) главную плоскость
, имеет в качестве сопряженного луч 1', который пересекает (непосредственно или при воображаемом продолжении) главную плоскость ![]() в точке
в точке ![]() , отстоящей в ту же сторону и на такое же расстояние от оси, как и точка
, отстоящей в ту же сторону и на такое же расстояние от оси, как и точка ![]() . Это легко понять, если вспомнить, что
. Это легко понять, если вспомнить, что ![]() и
и ![]() являются сопряженными точками, и учесть, что любой луч, проходящий через точку
являются сопряженными точками, и учесть, что любой луч, проходящий через точку ![]() , должен иметь в качестве сопряженного луч, проходящий через точку
, должен иметь в качестве сопряженного луч, проходящий через точку ![]() .
.
Поможем написать любую работу на аналогичную тему

