Дифракция сферических волн  от круглого отверстия

Поставим на пути сферической световой волны непрозрачный экран с вырезанным в нем круглым отверстием радиуса .

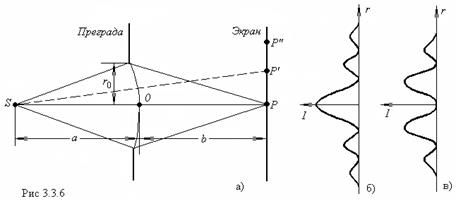
Расположим экран так, чтобы перпендикуляр, опущенный из источника света , попал в центр отверстия (рис.3.3.6).

На продолжении этого перпендикуляра возьмем точку .

При радиусе отверстия , значительно меньшем, чем указанные на рисунке длины  и :

- длину  можно считать равной расстоянию от источника  до преграды,

- длину  - расстоянию от преграды до точки .

Если расстояния  и  удовлетворяют соотношению

,

где  - целое число,

то отверстие оставит открытыми ровно  первых зон Френеля, построенных для точки .

Следовательно, число открытых зон Френеля определяется выражением

.

Амплитуда в точке  будет равна

.

Перед  берется знак

плюс, если  нечетное,  минус, если  четное.

Положив выражения в скобках равными нулю, придем к формулам

                 ( - нечетное),

            ( - четное).

Амплитуды от двух соседних зон практически одинаковы.

Поэтому  можно заменить через . В результате получится

,

где знак плюс берется для нечетных  и минус - для четных.

Для малых  амплитуда  мало отличается от .

Следовательно, при нечетных  амплитуда в точке  будет приближенно равна , при четных  - нулю.

Если убрать преграду, амплитуда в точке  станет равной .

Таким образом, преграда с отверстием, открывающим небольшое нечетное число зон:

• не ослабляет освещенность в точке ,
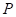• приводит к увеличению амплитуды почти в два раза, а интенсивности - почти в четыре раза.

Выясним характер дифракционной картины, которая будет наблюдаться на экране, помещенном за преградой (см. рис.3.3.6).

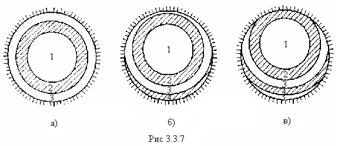
Вследствие симметричного расположения отверстия относительно прямой  освещенность в разных точках экрана будет зависеть только от расстояния  от точки :

Пусть, например, это число равно трем.

• Тогда в центре дифракционной картины получится максимум интенсивности. Картина зон Френеля для точки 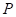 дана на рис. 3.3.7, а.
• Теперь сместимся по экрану в точку 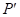. Ограниченная краями отверстия картина зон Френеля для точки  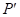имеет вид, показанный на рис. 3.3.7, б. :

Края отверстия закроют часть третьей зоны, одновременно частично откроется четвертая зона. В итоге интенсивность света уменьшится и при некотором положении точки  достигнет минимума.

• Если сместиться по экрану в точку 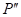, края отверстия частично закроют не только третью, но и вторую зону Френеля, одновременно откроется частично пятая зона (рис. 3.3.7, в). В итоге действие открытых участков нечетных зон перевесит действие открытых участков четных зон, и интенсивность достигнет максимума, правда, более слабого, чем максимум, наблюдающийся в точке .

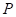Таким образом, дифракционная картина от круглого отверстия имеет вид чередующихся светлых и темных концентрических колец.

 В центре картины будет

• либо светлое ( 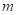нечетное),
• либо темное ( 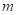четное) пятно.

Ход интенсивности  с расстоянием  от центра картины изображен

• на рис. 3.3.6,б (для нечетного )
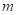• на рис. 3.3.6, в (для четного ).

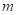 При перемещении экрана параллельно самому себе вдоль прямой  картины, изображенной на рис.3.3.7, будут сменять друг друга (при изменении  значение  становится то нечетным, то четным).

Если отверстие открывает

• лишь часть центральной зоны Френеля, на экране получается размытое светлое пятно; чередования светлых и темных колец в этом случае не возникает.
• большое число зон, чередование светлых и темных колец наблюдается лишь в очень узкой области на границе геометрической тени; внутри этой области освещенность оказывается практически постоянной.