Длина когерентности световых волн

В опыте Юнга интерференционная картина по мере удаления от ее середины размывается: несколько полос видны, но далее постепенно они исчезают.

Это происходит в результате того, что степень когерентности складываемых в этих точках экрана колебаний (волн) постепенно уменьшается, и колебания становятся наконец полностью некогерентными.

Пусть мы видим, например,

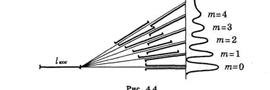
- первые четыре порядка интерференции (т = 4),

- затем полосы исчезают (этот переход наблюдается довольно плавным).

Исчезновение полос с т > 4 означает, что колебания, пришедшие в соответствующие точки экрана от обеих волн, оказываются уже некогерентными между собой. Т. е. пока их разность хода не превышает т = 4 длин волн, колебания в какой-то степени когерентны. Значит, вдоль распространения волны когерентными между собой будут только участки волны в этом интервале (длины). Данный интервал и называют длиной когерентности. В рассмотренном случае .

В данных условиях это простейший способ оценки длины когерентности:

,

 где т — максимальный порядок интерференции, соответствующий еще видимой светлой полосе.

Все это можно схематически представить с помощью рис. 4.4: в падающей на обе щели волне (рис. 4.3) длина когерентности , щели создают две волны с той же длиной когерентности, но поскольку они достигают разных точек экрана с различными разностями хода, то участки когерентности обеих волн постепенно сдвигаются относительно друг друга и, начиная с т = 5, перестают перекрывать друг друга — складываемые колебания становятся некогерентными и интерференционные полосы исчезают.

Все сказанное справедливо при условии, что «первичная» щель S достаточно узка. При расширении этой щели вступает в действие другой эффект.

Найдем выражение, определяющее .

Известно, что строго монохроматический свет — это идеализация.

Реальный свет, как бы ни стараться его монохроматизировать, остается в той или иной степени немонохроматическим, представляющим собой набор монохроматических компонент в некотором конечном интервале длин волн .

Примем, что эти монохроматические компоненты равномерно заполняют указанный интервал .

 :

• сплошными отрезками — для λ,
• пунктирными — для .

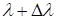Максимумы же от промежуточных длин волн заполняют интервал между крайними максимумами каждого порядка интерференции. В результате промежуточные максимумы, как видно из рисунка, будут постепенно заполнять интервал между максимумами соседних порядков для λ и .

это значит, что результирующие максимумы (нижняя часть рисунка) будут постепенно размываться, и полосы интерференции исчезнут.

Можно заключить, что полосы исчезнут там, где

,

 здесь т — предельный порядок интерференции, начиная с которого полосы исчезают. Отсюда

Величина характеризует степень монохроматичности света: чем она больше, тем больше и степень монохроматичности.

Значение т, при котором картина интерференции исчезает, т. е. складываемые колебания становятся уже некогерентными.

Найденное значение m связано с длиной когерентности как  .

 Отсюда следует, что

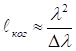
Длина когерентности световой волны непосредственно связана со степенью монохроматичности : чем больше  степень монохроматичности , тем больше и длина когерентности.

Для получения интерференционной картины, необходимо, чтобы оптическая разность хода складываемых колебаний  была меньше длины когерентности:

<

Это требование касается всех установок, с помощью которых наблюдают интерференционную картину.

Длина когерентности связана с так называемым временем когерентности τког — промежутком времени, в течение которого случайные изменения фазы световой волны в данной точке достигают значения порядка π.

За это время волна распространяется на расстояние порядка .