Обыкновенная и необыкновенная волны в основном порождаются разными цугами, ходящими в состав естественного света. Поэтому обыкновенная и необыкновенная волны, распространяющиеся в одноосном кристалле и выходящие их него при падении естественного света, некогерентны.
Однако обе волны можно сделать когерентными, если на пути естественного света установить поляризатор Р перед кристаллической пластинкой. При этом плоскость пропускания должна составлять с оптической осью кристалла угол 
(обычно 
). В этом случае колебания каждого цуга разделяются между обыкновенной о и необыкновенной е волнами, и волны о и е оказываются когерентными.
Интерференция не наблюдается, если складываемые волны поляризованы во взаимно перпендикулярных плоскостях. Чтобы изменить направление поляризации, необходимо на пути вышедшего из пластинки света поставить еще один поляризатор. Он сведет два взаимно ортогональных когерентных колебания в одну плоскость и интерференция будет обеспечена.
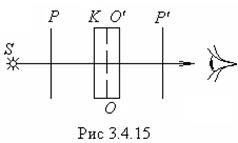
На рис.3.4.15 представлена схема наблюдения интерференции поляризованных волн:
S – обычный источник света,
Р – поляризатор,
К – кристаллическая одноосная пластинка,
Р¢ - второй поляризатор.
Если в качестве источника света взять лазер, то его излучение является плоскополяризованным, и необходимость поляризатора Р отпадает.
Картина интерференции будет наиболее отчетливой, когда амплитуды складываемых волн одинаковы. В этом случае угол между плоскостью пропускания поляризатора Р и оптической осью ОО¢ должен быть равен .
Рассмотрим частные случаи: когда плоскости пропускания обоих поляризаторов
1. параллельны друг другу (
)
2. взаимно перпендикулярны (
), в этом случае говорят, что поляризаторы скрещены.
1. 
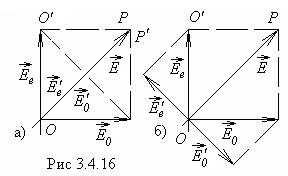
(рис.3.4.16,а).
Плоскополяризованная волна с амплитудой Е после поляризатора Р разделяется пластинкой на обыкновенную и необыкновенную взаимно ортогональные волны с амплитудами 
и 
.
Далее колебания этих волн приводятся поляризатором Р¢ к одной плоскости с одинаковыми амплитудами ¢ и ¢:
Результат интерференции этих волн зависит от разности фаз d, которую они приобретут в пластинке.
На рис.3.4.17 показана фазовая (векторная) диаграмма в предположении, что при прохождении пластинка обыкновенная волна отстает по фазе на d. По теореме косинусов имеем:
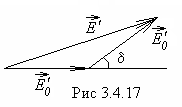
Интенсивность прошедшего света 
2. (рис.3.4.16,б).
В этом случае векторы 
и 
направлены взаимно противоположно. Поэтому кроме разности фаз d, вносимой пластинкой, необходимо добавить еще p, которая обусловлена скрещенным расположением поляризаторов.
Разность фаз равна d +p, и интенсивность 
Таким образом, интенсивности 
и 
оказываются «дополнительными»: в сумме они дают интенсивность света, прошедшего через поляризатор Р.
Интенсивность выходящего из поляризатора Р΄ света можно изменять, меняя разность фаз d. Этого можно достичь, меняя либо
- λ (это приводит к эффективному изменению окраски, т.е. максимумы пропускания будут соответствовать различным длинам волн),
- либо меняя толщину пластинки. Это можно сделать, поставив вместо пластинки компенсатор. В таблице приведены условия, при которых интенсивност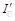и и 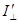достигают максимальных и минимальных значений.
|
Разность хода Δ |
тλ |
|
|
Разность фаз d |
2πт |
т΄π |
|
|
макс |
мин |
|
|
мин |
макс |
Поможем написать любую работу на аналогичную тему