 Рассмотрим две цилиндрические когерентные световые волны, исходящие из источников
Рассмотрим две цилиндрические когерентные световые волны, исходящие из источников ![]() и
и ![]() , имеющих вид параллельных тонких светящихся нитей (рис.3.2.4).
, имеющих вид параллельных тонких светящихся нитей (рис.3.2.4).
Область, в которой эти волны перекрываются, называется полем интерференции. Во всей этой области наблюдается чередование максимумов и минимумов интерференции.
Если в поле интерференции внести экран, на нем будет видна интерференционная картина, имеющая вид чередующихся темных и светлых полос.
Вычислим ширину этих полос, если экран параллелен плоскости, проходящей через источники ![]() и
и ![]() .
.
- Положение точки на экране будем характеризовать координатой х, отсчитываемой в направлении, параллельном прямой
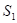
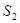 ,
, - начало отсчета выберем в точке О, относительно которой
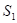 и
и 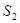 расположены симметрично.
расположены симметрично. - На рис.3.2.4
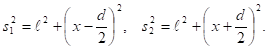
Тогда ![]()
- Для получения различимой интерференционной картины расстояние между источниками d должно быть значительно меньше расстояния до экрана
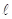 . (d<<
. (d<< 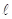 ).
). - Расстояние х, в пределах которого образуются интерференционные полосы, также много меньше
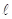 (х <<
(х << 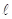 ).).
).).
Тогда ![]() , и
, и ![]() .
.
Умножив ![]() на показатель преломления среды п,
на показатель преломления среды п,
получим оптическую разность хода
![]() . (3.2.3)
. (3.2.3)
Подставив (3.2.3) в (3.2.1) и (3.2.2), получаем координаты максимумов и минимумов на экране:
![]()
где ![]() - длина волны в среде.
- длина волны в среде.
Расстояние между двумя соседними максимумами называется расстоянием между интерференционными полосами, а расстояние между двумя соседними минимумами – шириной интерференционной полосы. Эти расстояния имеют одинаковые значения
![]() . (3.2.4)
. (3.2.4)
Согласно (3.2.4),
- расстояние между полосами растет с уменьшением расстояния между источниками d.
- При d , сравнимом с
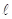 , расстояние между полосами было бы того же порядка, что и
, расстояние между полосами было бы того же порядка, что и 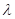 . В этом случае отдельные полосы были бы совершенно неразличимы.
. В этом случае отдельные полосы были бы совершенно неразличимы. - Чтобы интерференционная картина была отчетливой, необходимо, чтобы
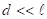 .
.
Если интенсивность интерферирующих волн одинакова, ![]() , то результирующая интенсивность в точках с разностью фаз
, то результирующая интенсивность в точках с разностью фаз ![]() равна
равна
![]() .
.
Т.к. ![]() , то согласно (3.2.3),
, то согласно (3.2.3), ![]() растет пропорционально х.
растет пропорционально х.
Следовательно, интенсивность меняется вдоль экрана по закону квадрата косинуса.
Ширина интерференционных полос и расстояние между ними зависят от длины волны ![]() .
.
- Только в центре картины, при х=0, совпадают максимумы всех длин волн.
- По мере удаления от центра максимумы разных цветов смещаются друг относительно друга все больше и больше. Интерференционная картина смазывается.
Поможем написать любую работу на аналогичную тему

