Понятие геометрической оптики

Длины воспринимаемых глазом световых волн очень малы (порядка  м). Поэтому распространение видимого света можно в первом приближении рассматривать, отвлекаясь от его волновой природы и полагая, что свет распространяется вдоль некоторых линий, называемых лучами. В предельном случае, соответствующем  , законы оптики можно сформулировать на языке геометрии. В соответствии с этим раздел оптики, в котором пренебрегают конечностью длин волн, называется геометрической оптикой. Другое название этого раздела - лучевая оптика.

Основу геометрической оптики образуют четыре закона: 1) закон прямолинейного распространения света; 2) закон независимости световых лучей; 3) закон отражения света; 4) закон преломления света.

Закон прямолинейного распространения утверждает, что в однородной среде свет распространяется прямолинейно. Этот закон является приближенным: при прохождении света через очень малые отверстия наблюдаются отклонения от прямолинейности, тем большие, чем меньше отверстие.

Закон независимости световых лучей утверждает, что лучи при пересечении не возмущают друг друга. Пересечения лучей не мешают каждому из них распространяться независимо друг от друга. Этот закон справедлив лишь при не слишком больших интенсивностях света. При интенсивностях, достигаемых с помощью лазеров, независимость световых лучей перестает соблюдаться.

Законы отражения и преломления света были сформулированы ранее.

В основу геометрической оптики может быть положен принцип Ферма: свет распространяется по такому пути, для прохождения которого ему требуется минимальное время.

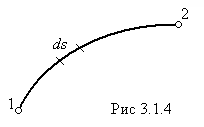
Для прохождения участка пути  ( рис.3.1.4 ) свету требуется время , где  - скорость света в данной точке среды. Заменив  через , получим, что .   Следовательно, время  , затрачиваемое светом на прохождение пути от точки 1 до точки 2, равно .  Имеющая размерность длины величина

называется оптической длиной пути. В однородной среде оптическая длина пути равна произведению геометрической длины пути  на показатель преломления среды : .

Отсюда .

Пропорциональность времени прохождения  оптической длине пути  дает возможность сформулировать принцип Ферма следующим образом: свет распространяется по такому пути, оптическая длина которого минимальна. Точнее, оптическая длина пути должна быть экстремальной, т. е. либо минимальной, либо максимальной, либо стационарной - одинаковой для всех возможных путей. В последнем случае все пути света между двумя точками оказываются таутохронными (требующими для своего прохождения одинакового времени).

Из принципа Ферма вытекает обратимость световых лучей. Действительно, оптический путь, который минимален в случае распространения света из точки 1 в точку 2, окажется минимальным и в случае распространения света в обратном направлении. Следовательно, луч, пущенный навстречу лучу, проделавшему путь от точки 1 к точке 2, пойдет по тому же пути, но в обратном направлении. Отставание по фазе , возникающее на пути с оптической длиной , определяется выражением

( - длина волны в вакууме).

Совокупность лучей образует пучок. Если лучи при своем продолжении пересекаются в одной точке, пучок называется гомоцентрическим. Гомоцентрическому пучку лучей соответствует сферическая волновая поверхность. На рис. 3.1.  5, а) показан сходящийся, а на рис.3.1. 5, б) - расходящийся гомоцентрический пучок. Частным случаем гомоцентрического пучка является пучок параллельных лучей; ему соответствует плоская световая волна.

Всякая оптическая система осуществляет преобразование световых пучков. Если система не нарушает гомоцентричности пучков, то лучи, вышедшие из точки , пересекутся в одной точке . Эта точка представляет собой оптическое изображение точки . Если любая точка предмета изображается в виде точки, изображение называется точечным или стигматическим.

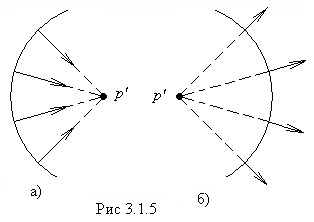Изображение называется действительным, если световые лучи в точке  действительно пересекаются (см. рис. 3.1.  5, а),  и мнимым, если в  пересекаются продолжения лучей, проведенные в направлении, обратном направлению распространения света (. рис. 3.1.  5. б).

Вследствие обратимости световых лучей источник света  и изображение  могут поменяться ролями - точечный источник, помещенный в , будет иметь свое изображение в . По этой причине  и  называются сопряженными точками.  Рис. 3.1.  5.

Оптическая система, которая дает стигматическое изображение, геометрически подобное отображаемому предмету, называется идеальной. С помощью такой системы пространственная непрерывность точек  отображается в виде пространственной непрерывности точек . Первая непрерывность точек называется пространством предметов, вторая — пространством изображений. В обоих пространствах точки, прямые и плоскости однозначно соответствуют друг другу. Такое соотношение двух пространств называется в геометрии коллинеарным соответствием.

Оптическая система представляет собой совокупность отражающих и преломляющих поверхностей, отделяющих друг от друга оптически однородные среды. Обычно эти поверхности бывают сферическими или плоскими (плоскость можно рассматривать как сферу бесконечного радиуса).

Оптическая система, образованная сферическими (в частности, плоскими) поверхностями, называется центрированной, если центры всех поверхностей лежат на одной прямой. Эту прямую называют оптической осью системы.

Каждой точке  или плоскости  в пространстве предметов соответствует сопряженная с ней точка  плоскость  в пространстве изображений. Среди бесконечного множества сопряженных точек и сопряженных плоскостей имеются точки и плоскости, обладающие особыми свойствами. Такие точки и плоскости называются кардинальными. К их числу относятся фокальные, главные и узловые точки и плоскости. Задание кардинальных точек или плоскостей полностью 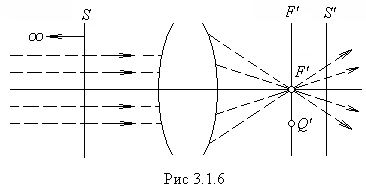определяет свойства идеальной центрированной оптической системы.