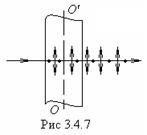
Рассмотрим кристаллическую пластинку, вырезанную параллельно оптической оси OO', на которую падает нормально линейно-поляризованный свет, плоскость поляризации которого составляет угол j с оптической осью пластинки (обычно j =45°).
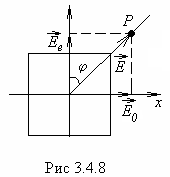рис.3.4.8 В кристалле в одном и том же направлении будут распространяться две волны с разными скоростями 
и 
, поляризованные взаимно ортогонально.
Р - плоскость поляризации падающего на пластинку света,
- его вектор-амплитуда,
OO' - оптическая ось кристалла,
и 
- векторы-амплитуды обыкновенной и необыкновенной волн в кристаллической пластинке.
В зависимости от толщины h пластинки обе волны выходят из пластинки с той или иной разностью фаз d, которая зависит от оптической разности хода данных волн, 
Разность фаз 
, где l - длина волны в вакууме, тогда
.
Итак, из кристаллической пластинки выходят две взаимно ортогональные плоскополяризованные волны:
- одна поляризована перпендикулярно к главному сечению кристалла,
- другая – в плоскости этого сечения , и в произвольной точке за кристаллической пластинкой соответствующие колебания светового вектора
. (3.4.2)
Будем считать, что оптическая разность хода обыкновенной и необыкновенной волн меньше длины когерентности, тогда обе волны будут когерентными, и разность фаз d не зависит от времени.
Характер поляризации результирующей волны зависит от толщины пластинки, которая и определяет разность фаз d.
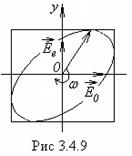Уравнение (3.4.2) – это уравнение эллипса в параметрической форме, поэтому вышедший из пластинки свет оказывается эллиптически поляризованным. Результирующий вектор вращается с угловой скоростью w, изменяясь при этом периодически по модулю (рис.3.4.9).
В зависимости от толщины пластинки h характер поляризации будет меняться.
Поможем написать любую работу на аналогичную тему