Решение задачи о дифракции Фраунгофера от щели методом графического сложения амплитуд

Разобьем открытую часть волновой поверхности на очень узкие зоны одинаковой ширины.

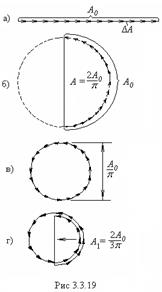Колебание, возбуждаемое каждой такой зоной, имеет одинаковую амплитуду  и отстает по фазе от предыдущего колебания на одну и ту же величину , зависящую от угла , определяющего направление на точку наблюдения . векторная диаграмма

• рис.3.3. 19, а

При . разность фаз  равна нулю.

Амплитуда результирующего колебания  равна сумме амплитуд складываемых колебаний.

• рис. 3.3.22, б 

при , колебания от краев щели находятся в противофазе.

Соответственно векторы  располагаются вдоль полуокружности длиной .

 Следовательно, результирующая амплитуда равна .

• на рис. 3.3.22.

при , колебания от краев щели отличаются по фазе на . Векторы  располагаются вдоль окружности длиной .

Результирующая амплитуда равна нулю - получается первый минимум.

• рис. 3.3.22, г

Первый максимум получается при .

 В этом случае колебания от краев щели отличаются по фазе на .

 Строя последовательно векторы , мы обойдем полтора раза окружность диаметра . Диаметр этой окружности и есть амплитуда первого максимума. Таким образом, интенсивность первого максимума равна . Аналогично можно найти и относительную интенсивность остальных максимумов.

В итоге получится следующее соотношение:

.

Таким образом, центральный максимум значительно превосходит по интенсивности остальные максимумы; в нем сосредоточивается основная доля светового потока, проходящего через щель.

В случае, когда ширина щели очень мала по сравнению с расстоянием от щели до экрана, лучи, идущие в точку  от краев щели, будут практически параллельными и в отсутствие линзы между щелью и экраном. Следовательно, при падении на щель плоской волны будет наблюдаться дифракция Фраунгофера. Все полученные выше формулы будут справедливыми, причем под  в этих формулах следует понимать угол между направлением от любого края щели к точке  и нормалью к плоскости щели.

Установим количественный критерий, позволяющий определить, какой вид дифракции будет иметь место в каждом конкретном случае.

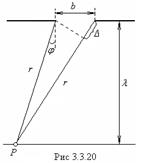
Найдем разность хода лучей от краев щели до точки  (рис.3.3. 22). Применим теорему косинусов к треугольнику со сторонами ,  и :

.

После несложных преобразований получим

.

Нас интересует случай, когда лучи, идущие от краев щели в точку , почти параллельны. При этом условии , поэтому в последнем уравнении можно пренебречь слагаемым . В этом приближении

.                                                         (3.3.6)

В пределе при  получается значение разности хода , совпадающее с выражением, фигурирующим в формуле (3.3.3).

При конечных  характер дифракционной картины будет определяться соотношением между разностью , и длиной волны .

 Если

,                                        (3.3.7)

дифракционная картина будет практически такой, как в случае дифракции Фраунгофера.

При  имеет место дифракция Френеля. В этом случае, согласно (3.3.6)

( - расстояние от щели до экрана).

Тогда из (3.3.7)   или.

Таким образом,

 характер дифракции зависит от значения безразмерного параметра .

Если этот параметр

• много меньше единицы, наблюдается дифракция Фраунгофера,
• порядка единицы - дифракция Френеля;
• много больше единицы, оказывается применимым приближение геометрической оптики.

Для удобства сопоставлений представим сказанное в следующем виде:

    .

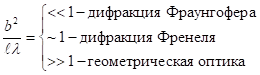Параметру  можно дать наглядное истолкование.

Возьмем точку , лежащую против середины щели (рис. 3.3.23). Для этой точки число  открываемых щелью зон Френеля определяется соотношением

.

Раскрыв скобки и отбросив слагаемое, пропорциональное , получим

.

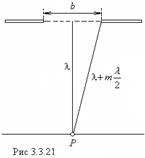Таким образом, параметр непосредственно связан с числом открытых зон Френеля (для точки, лежащей против середины щели).

• Если щель открывает малую долю центральной зоны Френеля 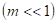, наблюдается дифракция Фраунгофера. Распределение интенсивности в этом случае изображается кривой, приведенной на рис.3.3. 22.
• Если щель открывает небольшое число зон Френеля 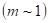, на экране получается изображение щели,  обрамленное по краям отчетливо видимыми светлыми и темными полосами.
• когда щель открывает большое число зон Френеля 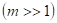, на экране получается равномерно освещенное изображение щели, лишь у границ геометрической тени имеются практически неразличимые глазом очень узкие чередующиеся более светлые и более темные полосы.

Проследим за видоизменениями картины при удалении экрана от щели. При небольших расстояниях экрана  от щели (когда ) изображение соответствует законам геометрической оптики. Увеличивая расстояние, мы придем сначала к френелевской дифракционной картине, которая затем перейдет во фраунгоферову картину. Та же последовательность превращений наблюдается в том случае, если, не изменяя расстояния , уменьшать ширину щели .

Из сказанного ясно, что критерием применимости геометрической оптики является не малость длины волны по сравнению с характерным размером преграды (например, шириной щели), а значение параметра  (он должен быть много больше единицы). Пусть, например, оба отношения  и  равны 100. В этом случае , однако =1 и, следовательно, будет наблюдаться отчетливо выраженная френелевская дифракция.