Фермионы и бозоны. Распределение Ферми-Дирака и  Бозе-Эйнштейна

Согласно современной квантовой теории все элементарные и сложные частицы, а также квазичастицы разделяются на два класса - фермионы и бозоны.

К фермионам относятся электроны, протоны, нейтроны и все другие частицы, имеющие полуцелые проекции спина, т.е. LSZ=±(2n+1)/2 , где n=0, 1, 2 ... - целые числа. Напомним, что спин (spin) LS    - это собственный момент импульса частиц, имеющий квантовую природу.

К бозонам относятся фотоны, некоторые ядра атомов, квазичастицы: фононы, магноны, плазмоны, экситоны. Все они имеют проекцию спина либо равную нулю, либо равную целому числу , т.е. LSZ=±n. Фермионы и бозоны имеют различные свойства.

Фермионы

Они подчиняются принципу Паули  - в одном квантовом состоянии может находится не более одного фермиона (или в одном квантовом состоянии может находиться только один фермион). Т.е. фермионы - индивидуалисты. Система фермионов описывается распределением Ферми-Дирака: среднее число фермионов <ni>, приходящееся на одно квантовое состояние с данной энергией Еi 

<ni>=,                                                                  (1)

где k - постоянная Больцмана, Т - термодинамическая температура, m - химический потенциал.

Поясним физический смысл химического потенциала. Известно, что первое начало термодинамики для системы с переменным числом частиц N имеет вид

dQ=dU+dA-mdN,                                                                                          (2)

отсюда изменение внутренней энергии dU=ТdS-PdV+mdN. Таким образом, слагаемое mdN учитывает изменение внутренней энергии системы за счет изменения числа частиц на dN.  Пусть протекает адиабатический (dQ=ТdS=0) изохорический (dV=0) процесс, тогда dU=mdN и химический потенциал          m= (dU /dN)S, V,

т. е. он характеризует изменение внутренней энергии системы dU  при добавлении в систему одной частицы, когда система при этом не получала тепла и не совершала работу; m  зависит от внешних параметров V, T  и числа частиц N. Для фермионов m>0.

На рис. 1(а) сплошной кривой представлено распределение Ферми-Дирака.

Если Т®0, то из (1) следует:

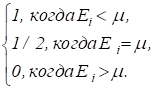áñ =                                        (3)

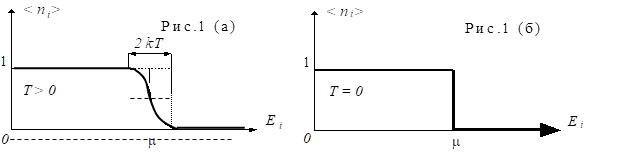Это значит, что при Т = 0 частицы Ферми - газа заполняют все квантовые состояния с энергиями  < m . Квантовые состояния с более высокими энергиями не заполнены. Кривая распределения вырождается в прямоугольник (рис. 1б).         Значение энергии, ниже которой все состояния системы частиц фермионов при Т = 0 К заняты, называется энергией  Ферми . Для идеального ферми газа  при Т = 0 К. Можно показать это

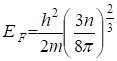                             ,                                                  (4)           

где m и n - масса и концентрация фермионов. Следовательно, максимальная энергия, которую могут иметь электроны в металле при Т = 0 К, равна энергии Ферми . Для хорошо проводящих металлов , для полупроводников - значительно  меньше

 Бозоны

Они не подчиняются принципу Паули, т. е. в одном квантовом состоянии может быть много бозонов, т. е. бозоны - коллективисты. Система бозонов  описывается распределением Бозе-Эйнштейна: среднее число бозонов áñ, приходящееся на одно квантовое состояние с энергией                                     

                            (5)

Поскольку числа заполнения áñ не могут быть отрицательными, то из (5) следует, что для бозонов m £0. Распределение Бозе-газа представлено на рис.2.

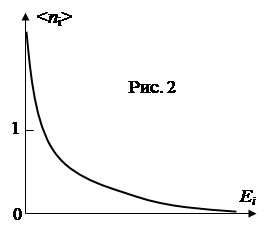
Физическая природа двойного лучепреломления

Особенности распространения света в среде определяются интерференцией первичной и вторичной волн, излучаемых молекулами вещества в результате их электронной поляризации под действием электрического поля  световой волны. Поэтому оптические свойства среды полностью характеризуется электрическими свойствами молекул (атомов, ионов), их взаимным расположением и взаимодействием друг с другом. Если молекулы электрически изотропны, то их свойства (поляризуемость) не зависят от направления; если анизотропны - зависят.

 Оптическая анизотропия кристалла может быть обусловлена как электрической анизотропией образующей его частиц, так и анизотропией поля сил взаимодействия между частицами.

Анизотропность этого поля зависит от степени симметрии решётки кристалла. Изотропнны только кристаллы, имеющие кубическую решётку (например, NaCl).

Будем рассматривать кристалл как однородную среду

Оптическая анизотропия немагнитных кристаллов является следствием анизотропии их относительной диэлектрической проницаемости.

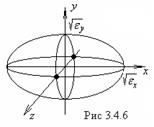рис. 3.4.6 Рассмотрим оптически однородную среду, которая не поглощает электромагнитные волны  и оптически неактивна.

проведём из точки О по всем направлениям радиусы-векторы ,

где  - значение диэлектрической проницаемости в данном  направлении. Поверхность, проходящая через концы радиусов - векторов , имеет форму эллипсоида и называется оптической индикатрисой среды. Оси симметрии этого эллипсоида взаимно перпендикулярны и определяют три главных направления в среде.

Линейно поляризованная плоская монохроматическая волна в анизотропной среде характеризуется двумя тройками векторов: () и ().

Векторы  и  лежат в одной плоскости, перпендикулярной вектору , вектор  - скорость распространения волновой поверхности вдоль нормали к ней, .

Скорость  называется нормальной скоростью волны.

Скорость - лучевая скорость волны, она совпадает по направлению с вектором Пойтинга  и равна скорости переноса энергии волной, причем

,

Скорость   в направлении вектора :

где n - абсолютный показатель преломления среды для волны с заданным направлением вектора .

Если  совпадает с одним из главных направлений, то луч совпадает с нормалью к фронту волны, а лучевая скорость волны равна фазовой:

где  - главные значения показателя преломления анизотропной среды.

В анизотропном кристалле всякая плоская монохроматическая волна распадается на две плоские волны (обыкновенную и необыкновенную), которые линейно поляризованы во взаимно перпендикулярных плоскостях и обладают различными нормальными и лучевыми скоростями.

В обыкновенной волне :

• вектор 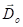 перпендикулярен к оптической оси кристалла и к направлению единичного вектора  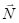нормали к фронту волны.
• Нормальная скорость этой волны

,

 где   показатель преломления кристалла для обыкновенной волны.

• В одноосном кристалле любое направление, перпендикулярное к оптической оси, является главным, поэтому в обыкновенной волне векторы 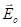и 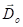 взаимно параллельны, и обыкновенный луч совпадает с нормалью  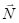к фронту волны, лучевая скорость

,

 является показателем преломления кристалла для обыкновенного луча.

Т.е. обыкновенная волна распространяется в анизотропной среде так же, как в изотропной, поэтому она называется обыкновенной.

В необыкновенной волне:

• вектор 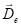 перпендикулярен к  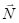и 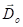, т.е лежит в плоскости, проходящей через оптическую ось и нормаль .
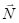• Нормальная скорость этой волны

, ее модуль ,

где ne- показатель преломления кристалла для необыкновенной волны,

он зависит от направления нормали .

• Плоскость, проходящая через луч и пересекающую его оптическую ось кристалла, называют главной плоскостью одноосного кристалла для этого луча. Обыкновенный луч поляризован в главной плоскости ( 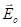перпендикулярен к этой плоскости), а необыкновенный луч поляризован в плоскости, перпендикулярной к главной плоскости (вектор  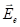лежит в главной плоскости).

Лучевая скорость для необыкновенного луча

.

Лучевые скорости  и  называются скоростями распространения обыкновенного и необыкновенного лучей.

Различие в величинах  и  обуславливает двойное луче преломление света в одноосном кристалле.

 Двойное лучепреломление отсутствует, когда свет падает нормально на плоскую поверхность кристалла, перпендикулярную к его оптической оси – вдоль оптической оси обыкновенный и необыкновенный лучи распространяются с одинаковыми скоростями.

 В двуосных кристаллах скорости распространения обоих лучей зависят от направления распространения в кристалле, поэтому оба луча являются необыкновенными. Вдоль каждой из оптических осей кристалла двойное лучепреломление отсутствует.