Формула оптической системы

Задание кардинальных плоскостей или точек полностью определяет свойства оптической системы. В частности, зная положение кардинальных плоскостей, можно построить оптическое изображение, даваемое системой. Возьмем в пространстве предметов отрезок , перпендикулярный к оптической оси (рис. 3.1. 11; узлы на рисунке не показаны). Положение этого отрезка можно задать либо расстоянием , отсчитанным от точки  до точки , либо расстоянием  от  до . Величины  и , как и фокусные расстояния  и  являются алгебраическими (на рисунках указываются их модули).

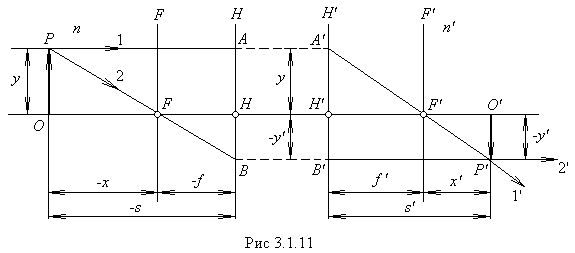Проведем из точки  луч 1, параллельный оптической оси.  Он пересечет плоскость  в точке .  В соответствии со свойствами главных плоскостей сопряженный лучу 1 луч 1' должен проходить через сопряженную с точкой  точку  плоскости .  Так как луч 1 параллелен оптической оси, сопряженный с ним луч 1' пройдет через задний фокус . Теперь проведем из точки  луч 2, проходящий через передний фокус . Он пересечет плоскость  в точке . Сопряженный с ним луч 2' пройдет через сопряженную с  точку  плоскости  и будет параллельным оптической оси. Точка  пересечения лучей 1' и 2' представляет собой изображение точки . Изображение , как и отрезок , перпендикулярно к оптической оси.

Положение изображения  можно охарактеризовать либо расстоянием  от точки  до точки , либо расстоянием  от  до . Величины  и  являются алгебраическими. В случае, изображенном на рис. 3.1. 11, они положительны.

Величина , определяющая положение изображения, закономерно связана с величиной , определяющей положение предмета, и с фокусными расстояниями  и . Для прямоугольных треугольников с общей вершиной в точке  (рис. 3.1. 11) можно написать соотношение

.

Аналогично, для треугольников с общей вершиной в точке  имеем

.

Объединив оба соотношения, получим что , откуда

.                                                 (3.1.27)

Это равенство называется формулой Ньютона. При условии, что , формула Ньютона имеет вид

.                                               (3.1. 28 )

От формулы, связывающей расстояния  и  предмета и изображения от фокусов системы, легко перейти к формуле, устанавливающей связь между расстояниями  и  от главных точек. Из рис. 3.1. 11 видно, что  (т. е. ), . Подставив эти выражения для  и  в формулу ( 14 ) и произведя преобразования, получим

.                                             (3.1. 29 )

При выполнении условия  формула (3.1.29  ) упрощается следующим образом:

.                                             ( 3.1.30 )

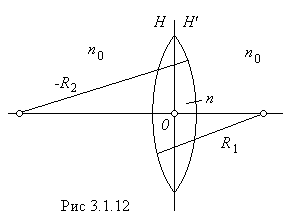Соотношения ( 3.1.27 ) – ( 3.1.30 ) представляют собой формулы центрированной оптической системы.