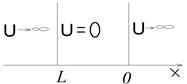При движении свободной частицы (U(x)=0) ее полная энергия совпадает с кинетической. Для свободной частицы движущейся вдоль оси х стационарное уравнение Шредингера 
переходим к решению уравнения второго порядка 
,обозначим
=>
решением этого уравнения получаем 
или
подчиняя 
граничным условиям 1)
получим 
тогда 
2) 
выполняется только при 
где n – целые числа
подставим 
=>
=>
т.е. стационарное уравнение Шредингера описывающее движение частицы в «потенциальной яме» с бесконечно высокими «стенками» удовлетворяется только при собственных значениях Еп
зависящих от целого числа п => Еп принимает лишь определенные дискретные значения , т.е. квантуются. Квантовые значения энергии Еп называются уровнями энергии а число п определяющее энергетические уровни частицы называется главным квантовым числом
энергетический интервал между двумя соседними энергетическими уровнями равен 
Поможем написать любую работу на аналогичную тему