Разделение зарядов

Рассмотрим масштаб разделения зарядов во времени. Пусть в плазме в результате разделения зарядов возник объёмный заряд с плотностью . По закону сохранения заряда:

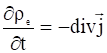                                        ,                                               (1)

где  – плотность тока. Если ток переносится только электронами, то:

                                                   ,                                              (2)

где  – скорость электронов, переносящих ток.

Уравнение движения электрона:

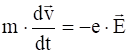                                      .                                             (3)

Из (1)-(3) имеем:

                                  .

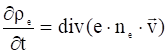Продифференцируем по времени, получим:

                                ,

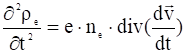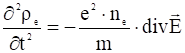                                .                                       (4)

При этом, имея в виду линейные колебания и не делая различия между частотой и полной производной по времени, мы отбросили все квадратичные члены, а не вынесли за знаки дифференциалов.

По уравнению Максвелла:

                                       ,

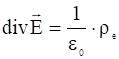тогда:

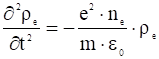                                              .                                          (5)

Полученное уравнение описывает гармонические колебания с частотой:

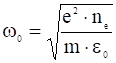                                                  .                                              (6)

Частота  называется плазменной частотой.

Таким образом, в случае разделения в плазме зарядов возникающие электростатические силы вызывают так называемые электростатические, или ленгмюровские колебания. Электростатические колебания были обнаружены Ленгмюром и Томпсом (1929 г.) в газовом разряде.

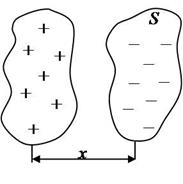
Возникновение плазменных колебаний объясняется следующим образом: локальное нарушение квазинейтральности происходит в результате смещения электронов из слоя толщиной  на одну из «ограничивающих» этот слой плоскостей, при этом образуется как бы «конденсатор». Заряд этого конденсатора равен:

                                     ,
ёмкость:

                                          ,
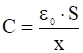а разность потенциалов:

                                   .

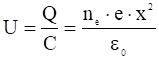Величина однородного электрического поля между пластинами конденсатора:

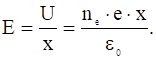
Это поле сообщает каждому электрону ускорение

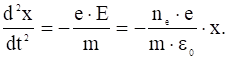
Полученное уравнение описывает колебания с частотой:

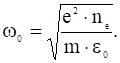
Отметим, что у плазмы много различных типов колебаний, особенно, если она помещена в магнитное поле. Но плазменными колебаниями принято называть не всякие колебания плазмы, а именно электростатические колебания с частотой . Таким образом, «плазменные колебания» и «колебания плазмы» – не одно и то же. Термин «колебания плазмы» имеет более широкий смысл. Плазменные колебания не имеют волнового характера – нарушения электронейтральности не распространяются по плазме.

Временной масштаб разделения зарядов есть величина того же порядка, что и период плазменных колебаний:

                                            .                                                   (7)
Разделение зарядов может быть существенным только за периоды времени, малые по сравнению с этим масштабом.

За пространственный масштаб разделения зарядов  можно принять расстояние, которое частица при своём тепловом движении проходит за время :

                                            ,                                                   (8)
где  – средняя скорость теплового движения частиц.

В масштабах, больших по сравнению с , соблюдается квазинейтральность.

Пространственный масштаб разделения зарядов можно рассмотреть и с энергетической точки зрения. В электрическом поле чтобы преодолеть разность потенциалов  электрон должен обладать энергией

                                 ε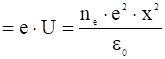.                                        (9)

Расстояние, на котором может быть заметным разделение зарядов вследствие теплового движения, определяется тем условием, что энергия (9) должна быть одного порядка с энергией теплового движения . Тогда расстояние , на котором возможно заметное разделение зарядов, находится из условия:

                                    ,

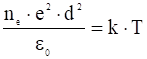откуда:

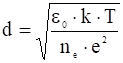                                      .                                           (10)

Разделив числитель и знаменатель под корнем на  и подставив вместо средней скорости теплового движения близкую к ней величину , можно убедиться, что выражение (10) тождественно формуле (8).

Для плазмы, имеющей определённую температуру, выражение (8) следует рассматривать как приближение, а (10) – как точное. Но поскольку плазма часто не находится в состоянии термодинамического равновесия, то понятие температуры теряет для неё строгий смысл. В этом случае пространственный масштаб  разделения зарядов для частиц каждого рода определяется формулой (8).

Пространственный масштаб  разделения зарядов называют также поляризационной длиной, так как это наибольшая длина, на которой вследствие теплового движения самопроизвольно возникают разности потенциалов, то есть происходит поляризация плазмы. В частности, у границы плазмы возникает слой, в котором квазинейтральность нарушается, причём толщина этого граничного слоя порядка пространственного масштаба разделения зарядов.

Если разделение зарядов происходит в результате смещения электронов, то найденную частоту  называют электронной плазменной частотой, а соответствующий пространственный масштаб разделения зарядов – электронной поляризационной длиной. Можно найти аналогичные величины, принимая, что разделение зарядов вызывается движением ионов, тогда получается ионная плазменная частота. Поскольку электроны подвижнее ионов, то электронная плазменная частота важнее ионной. Если говорят просто о плазменной частоте, то имеют в виду электронную плазменную частоту.