Если учесть конечную проводимость, то условие (5) уже не будет удовлетворяться. В системе координат, связанной с плазмой, будут действовать электрические поля, вызывающие электрические токи. В приближении магнитной гидродинамики ток считается подчиняющимся закону Ома:
, (6)
здесь 
– проводимость (в этом приближении считается скалярной величиной).
Для плазмы, находящейся в магнитном поле, закон Ома (6) является приближённым, так как он не учитывает анизотропию проводимости.
Из (6) следует, что:
.
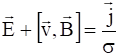Воспользуемся уравнением Максвелла, пренебрегая токами смещения:
.
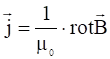После подстановки имеем:
.
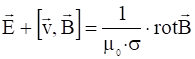Применим операцию 
к обеим частям полученного равенства:
.
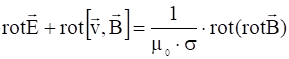Воспользуемся уравнением Максвелла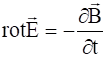 
и формулой векторного анализа 
, и учитывая, что 
, получим:
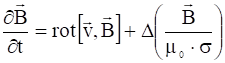. (7)
Рассмотрим простейший случай, когда движение вещества отсутствует, то есть 
. Тогда:
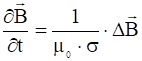. (8)
Это уравнение тождественно по виду с уравнением диффузии (второй закон Фика), роль коэффициента диффузии играет величина:
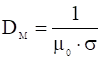, (9)
обратно пропорциональная проводимости плазмы. Можно сказать, что из-за конечной проводимости магнитное поле как бы просачивается сквозь плазму по диффузионному закону с коэффициентом диффузии 
.
Глубина просачивания поля в течение заданного времени 
:
.
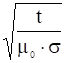Для переходного процесса время порядка обратной частоты 
и, следовательно:
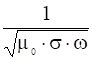. (10)
называют толщиной скин-слоя, а в более общем случае непериодических процессов выражение (10) называют выражением для скиновой длины. Можно оценить время просачивания магнитного поля на заданную глубину :
,
эту величину называют скиновым временем.
Поможем написать любую работу на аналогичную тему