Электростатическое экранирование

Рассмотрим электростатическое экранирование отдельной заряженной частицы в плазме. В пустом пространстве вокруг частицы с зарядом электростатический потенциал:

                                    .

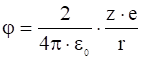В плазме заряженная частица вызывает поляризацию окружающей плазмы: вокруг такой частицы скапливаются частицы противоположного знака, экранирующие поле частицы. Экранированный потенциал можно вычислить с помощью теории Дебая, развитой им первоначально для растворов сильных электролитов. Эта теория основана на представлении о самосогласованности поля: находят такое распределение электрического поля, которое создаёт распределение частиц, возбуждающее в свою очередь заданное поле.

Запишем уравнение Пуассона:

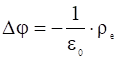                                                                                   (12)
и распределение Больцмана:

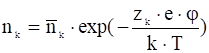                              ,                                   (13)
здесь  – концентрация частиц с зарядовым числом  в точке с потенциалом ;                                                                   
 – концентрация тех же частиц в точке с нулевым потенциалом (её приравнивают к средней концентрации, взятой по всему объёму).

Индексом  отмечены все частицы, включая электроны, для которых . Средние концентрации удовлетворяют условию квазинейтральности:

                                        .                                             (14)

Объёмный заряд:

                                     .                                          (15)

Запишем нелинейное уравнение самосогласованного поля:

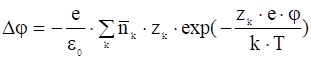                   .                        (16)

Однако в таком нелинейном виде пользоваться уравнением не имеет смысла. Дело в том, что распределение Больцмана даёт вероятность нахождения частицы в точке с потенциалом , то есть среднее по времени значение концентрации, но мгновенные концентрации случайным образом меняются (флуктуируют) вокруг этого среднего значения, вызывая соответствующие флуктуации потенциала. Если в (16) под  подразумевать среднее по времени значение , то окажется, что в правой части среднее значение функции заменено функцией от среднего значения, что допустимо только для линейных функций. Поэтому (16) может быть использовано только в линейном приближении. Для линеаризации раскладываем в правой части (16) экспоненциальные функции в ряд, сохраняя только линейные члены, получим линейное уравнение самосогласованного поля:

                                                      
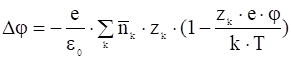
и учитывая (14), приходим к выражению:

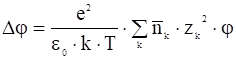                           .                                (17)

Решение уравнения (17) для симметричного распределения потенциала вокруг точечного заряда имеет вид:

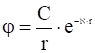                                         ,                                              (18)
где  – постоянная экранирования:

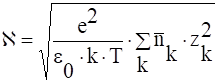                             .                                  (19)
(;
в сферических координатах:               
         ).

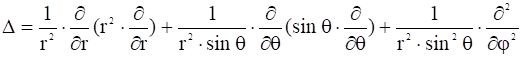Постоянная  в (18) должна быть такой, чтобы на малых расстояниях потенциал стремился к значению , определяемому для частицы в пустом пространстве. Отсюда следует окончательное выражение для экранированного потенциала вокруг заряженной частицы в плазме:

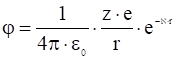                                 .                                      (20)

Величина 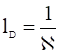 называется длиной экранирования или дебаевской длиной (радиус Дебая-Хюккеля). Легко видеть, что она получается из введённых выше пространственных масштабов разделения зарядов  по правилу сложения обратных квадратов:

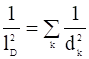                                          .                                               (21)

Поэтому длину экранирования можно рассматривать как пространственный масштаб разделения зарядов или поляризационную длину для всей плазмы в целом.

Теперь можно дать определение плазмы, в котором устанавливается количественный смысл её квазинейтральности.

Плазма – это ионизованный газ, для которого дебаевский радиус мал в сравнении с линейным масштабом области, занимаемой газом. Такое определение дано И. Ленгмюром.