Шкалограмма Гуттмана. Суть подхода к измерению латентной переменной

Известный американский психолог Л. Гуттман предложил свой способ адаптации тестовой традиции к потребностям социологии . В принципе идея была той же — опереться на проверку того, что наблюдаемые признаки представляют собой плотную связку в смысле корреляции друг с другом, и предложить такой способ измерения латентной переменной, чтобы при фиксации ее значения эти корреляции исчезали. Описание метода можно найти в .

Наблюдаемые признаки — дихотомические. Предполагается, что выполнение условий, требующихся для реализации тестовой традиции, будет обеспечено, если удастся доказать возможность определенным образом их упорядочить. А именно: будем говорить, что признаки упорядочены, если, скажем, относительно человека, положительно реагирующего на третий признак, можно быть почти уверенным, что он положительно реагировал и на четвертый, пятый и т.д. признаки.

Подобные шкалы называются кумулятивными. Они использовались и до Гуттмана. Так, кумулятивна известная шкала социальной дистанции Богардуса, содержащая семь признаков, отражающих различные степени социальной дистанции. Эти признаки могут быть следующим образом упорядочены (речь идет об отношении респондента к человеку или социальной группе, дистанция до которой вычисляется): допущение человека в качестве родственника посредством брака, как личного друга, в качестве соседа, допущение равной работы, гражданства, допущение в страну только в качестве туриста. Кумулятивность шкалы представляется очевидной: относительно респондента, согласного принять кого-то в качестве соседа, можно почти наверняка сказать, что он согласится с тем, чтобы тот же человек имел одинаковые с ним работу, гражданство, или мог приехать в страну как турист.

Значение латентной переменной рассчитывается как сумма положительных ответов, данных респондентом на рассматриваемые вопросы. Нетрудно показать, что если рассматриваемые дихотомические признаки удалось упорядочить, то соответствующая матрица данных приведется к так называемому диагональному виду (табл. 7.2).

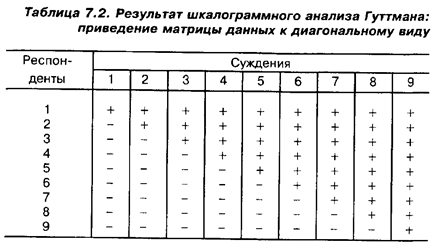
Плюсами помечены положительные ответы респондентов на соответствующие вопросы анкеты (их согласие с соответствующими суждениями), минусами — отрицательные.

Нетрудно проверить, что согласие респондента, скажем, с 4-м суждением означает его согласие с 5-м, 6-м и т.д. А это и означает, что наши признаки упорядочены.

Но поскольку количество респондентов, как правило, будет больше числа суждений, то многие респонденты будут давать одинаковые наборы ответов, и матрица приобретет ступенчато-диагональный вид (табл. 7.3).

Нетрудно показать, что для таких переменных будут выполнены все требующиеся посылки: они будут связаны друг с другом и фиксация значения латентной переменной приведет к распаду этих связей.

Таблица 7.3. Результат шкалограммного анализа Гуттмана: приведение матрицы данных к ступенчато-диагональному виду

Если взять только тех людей, которые имеют одно и то же значение латентной переменной, то для них однозначно восстанавливается картина их ответов на рассматриваемые вопросы: балл 5 респондент может иметь только в том случае, если он дал положительные ответы на последние 5 вопросов. Другими словами, респонденты с одним и тем же значением латентной переменной имеют одни и те же значения рассматриваемых признаков. Ни о какой связи тут говорить не приходится.

Гуттман предложил простой алгоритм, позволяющий либо привести матрицу к диагональному виду, либо показать, что это сделать в принципе невозможно. Прежде чем описать этот алгоритм, заметим, что мы должны учитывать еще одно обстоятельство.

Выше в действительности был описан некий идеальный случай. Мы уже говорили, что в социологии практически никакая теоретическая схема никогда не проходит в совершенно чистом виде, никакая гипотеза не может стопроцентно выполняться, никакие данные не бывают без ошибок. И всегда встает вопрос, в каких пределах эти ошибки допустимы.

В нашем случае это означает, что даже при самом тщательном подборе суждений всегда найдутся респонденты, для которых они не будут упорядочены предполагаемым нами образом. То есть наша матрица хотя бы в малой мере, но практически всегда не будет точно диагональной. Необходимо, как всегда в подобных случаях, установить предел допустимых ошибок. В ситуации, когда этот предел не будет превышен, считать, что матрица диагональна, и, следовательно, наши условия, обеспечивающие возможность использования тестовой традиции, выполняются. Если ошибки превысят допустимый предел, то будем полагать, что матрицу нельзя привести к диагональному виду и, стало быть, нельзя описанным образом измерять латентную переменную.

Ошибки будут проявляться в том, что даже в самом хорошем варианте у нас в области плюсов будут одиночные минусы, и наоборот. Оценим количество таких смешений. Их ниже мы и называем ошибками. Введем критерий:

R = 1 — (количество ошибок)/(количество клеток в таблице).

Будем полагать, что мы привели матрицу к диагональному виду, если R < 0,9. Теперь на примере покажем, в чем состоит алгоритм Гуттмана и как можно оценить качество его работы.

Итак, пусть исходная матрица данных имеет вид (табл. 7.4).

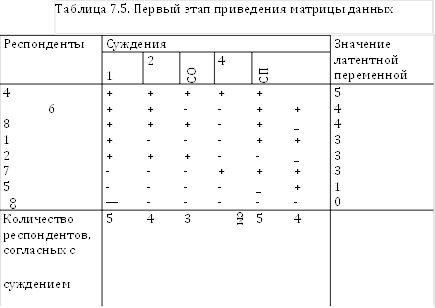
Таблица 7.4. Фрагмент гипотетической матрицы данных, полученных с помощью шкалы Гуттмана

В соответствии с упомянутым алгоритмом сначала надо таким образом переставить строки, чтобы соответствующие им значения измеряемой переменной расположились по убыванию (табл. 7.5).

Не зря мы ввели в таблицу еще одну строку. Теперь надо переставить столбцы таблицы таким образом, чтобы возрастали ранги, стоящие в ее нижней, как бы маргинальной, строке (табл. 7.6).

Строго диагонального (ступенчато-диагонального) вида у нас не получилось. Теперь требуется оценить, можно ли все же считать, что полученная матрица достаточно близка к диагональному виду.

R = I - (6 + 3)/ 48 = 0,81

(6 — количество плюсов, заблудившихся в минусовой области; 3 — количество минусов, находящихся в плюсовой области). Если такое значение критерия представляется неприемлемым (19% неправильных клеток в таблице), то приходим к выводу, что наша гипотеза о наличии латентной переменной, проявляющейся в рассматриваемых наблюдаемых признаках, не верна.

Итак, наша работа начинается с того (имеется в виду этап работы после предварительного формирования анкеты), что мы проводим пробное исследование, собираем данные и переставляем столбцы и строки полученной матрицы до тех пор, пока она либо приобретет диагональный вид, либо мы убедимся в том, что это сделать невозможно. В первом случае мы полагаем, что одномерная латентная переменная существует, признаки и способ выражения через них латентной переменной выбраны удачно, и переходим к основному исследованию. Во втором — вообще говоря, отказываемся от построения одномерной шкалы. Однако в отдельных случаях исправить положение можно с помощью некоторой корректировки данных. Скажем, может оказаться, что привести матрицу к диагональному виду нам мешает какой-то ее столбец. Тогда выбросим из рассмотрения соответствующее суждение: оно не укладывается в наше упорядочение (может быть, не так понимается респондентами, как мы рассчитывали, и т.д.). Затем перейдем к основному исследованию. В приведенном выше примере таким суждением можно считать шестое (правда, убрав его, мы уменьшим долю неправильных клеток не до 10%, а только до 12% (стало быть, R будет равно 0,88).

Может оказаться и так, что нам мешает строка матрицы, т.е. какой-то респондент. Можно отбросить и его и двигаться дальше. Но здесь надо быть осторожными, о чем мы уже говорили.