Приложение 1. Внеклассное мероприятие по математике для старших классов на тему: «По страницам истории»

Тема: По страницам истории.

Девизы урока: 

                                О, сколько нам открытий чудных…

                                                                                                     Пушкин А.С.

                                Три пути ведут к знанию:

                                Путь размышления – самый благородный,

                                Путь подражания – самый легкий

                                И путь опыта – это путь самый горький…

                                                                                            Конфуций

Цель урока: 

1) Развить творческую активность;

        2) показать нестандартные способы решения задач по теории                                             вероятностей;

       3) побудить интерес к теории вероятностей, математике.

      Учитель объявляет тему урока, зачитывает девизы, подчеркнув лаконичность, целенаправленность, точность народной мудрости и соответствие выбранных изречений задачам урока. Обращает внимание учеников на то, что математика много дает для умственного развития человека – заставляет думать, соображать, искать простые и красивые решения, помогает развивать логическое мышление, умение правильно и последовательно рассуждать, тренирует память, внимание, формирует многие учебные навыки и умения, закаляет характер.  Учитель знакомит учащихся со старинными задачами науки о случайном – показывает связь прошлого с современностью.    

    Учитель: Еще в глубокой древности появились различные игры. В Древней Греции и Риме широкое распространение получили игры в астрагалы (то есть бросание костей из конечностей животных) и игральные кости (кубики с нанесенными на гранях точками). В настоящее время игральные кости иногда изготовляют в виде додекаэдров и икосаэдров.  В одной из азартных (слово «азартный» происходит от арабского «азарт» - трудный, то есть редко выпадающие комбинации костей) игр бросали одновременно четыре астрагала и фиксировался результат. Худший бросок, при котором выпадает более одной единицы, назывался «собакой». Лучшим броском считался бросок «Венера», когда на четырех астрагалах выпадали различные грани. Позднее азартные игры распространились в Средневековой Европе. В частности, в XIV веке появились игральные карты. В  XVII веке азартные игры способствовали зарождению и становлению комбинаторики и науки о случайном (теории вероятностей). Ученые XV-XVII веков много внимания уделяли решению задач о дележе ставки, об игре в кости, лотереях и т. п.

                                     Задачи о дележе ставки.

До середины XVII не было правильных   задач о справедливом разделении ставки. В 1654 году между французским математиком Блезом Паскалем и Пьером Ферма возникла переписка по поводу ряда задач. Из переписки Паскаля и Ферма сохранилось лишь 3 письма Паскаля и 4 письма Ферма. Эти письма впервые были опубликованы в Тулузе. В этой переписки оба ученых, хотя и несколько разными путями, приходят к верному решению, деля ставку пропорционально вероятности выиграть всю ставку, если игра будет продолжена.

      Совпадение результатов великих ученых при решении задач о дележе ставки послужило для Паскаля поводом шутливо заметить в первом письме к Ферма от 29 июля 1654 года: «Как я вижу, истина одна: и Тулузе, и в Париже ». Ферма со своей стороны нашел решение и для более сложного случая, когда игра происходит между произвольным числом игроков.

Задачи Блеза Паскаля. Как разделить ставку при игре трех выигрышных партий, если один игрок выиграл две партии, а другой – одну и  каждым вложено в игру по 32 пистоля ?

Решение.

Свое решение задачи Паскаль наиболее полно изложил в письме  к Ферма от 29 июля 1654 года: « Вот примерно, что я делаю для определения стоимости каждой партии, когда два игрока играют, например, на три партии и каждым вложено в игру по 32 пистоля.

Предположим, что один выиграл две партии, а другой – одну. Они играют еще одну партию, если ее выигрывает первый, то он получает всю сумму в 64 пистоля…; если же  эту партию выигрывает второй, то каждый игрок будет иметь  две выигранные партии, и, следовательно, если они намерены произвести раздел, каждый должен получить обратно свой вклад в 32  пистоля.

Примите же во внимание, монсеньер, что если первый выиграет, то ему причитается 64; если он проиграет, то ему причитается 32. Если же игроки не намерены рисковать… и хотят произвести раздел, то первый должен сказать : «Я имею 32 пистоля верных, ибо в случае проигрыша я их также получил бы, но остальные 32 пистоля могут быть получены либо мной, либо Вами. Случайности равны. Разделим же эти 32 пистоля пополам, и дайте мне , кроме того, бесспорную сумму в 32 пистоля». Как видно из рассуждений Паскаля, первый игрок должен получить 48 пистолей, а второй - 16».

1.  Как разделить ставку при игре трех выигрышных партий, если один игрок выиграл две партии, а другой – ни одной и каждым вложено в игру по 32 пистоля ?

Решение.

Ответы, предложенные паскалем, таковы: первый игрок должен получить 56 пистолей, а второй – 8. рассуждения при решении подобны тем, которые были проведены при решении предыдущей задачи: если бы первый игрок выиграл еще одну партию, то ему причиталось бы 64 пистоля, если бы проиграл – 48 пистоля, а остаток 16 делится поровну.

2.  Как разделить ставку при игре трех выигрышных партий, если первый игрок выиграл одну партию, а второй- ни одной и  каждым вложено в игру по 32 пистоля ?

Решение.

Пусть игроки сыграют еще одну партию. Если ее выиграет первый, то он будет иметь , как и в предыдущем случае, 56 пистолей. Если он ее проиграет, то у обоих окажется по одной выигрышной партии и первому следует получить 32 пистоля. Первый игрок может сказать: «Если вы не хотите играть эту партию, дайте мне мой бесспорный выигрыш в 32 пистоля, а остаток от 56 пистоля  разделим поровну…то есть возьмем каждый по 12 пистолей, что с 32 пистолей составит 44 пистоля». Значит, первый игрок должен получить 44  пистоля, а второй – 20 пистолей.

Для случая, когда первый игрок выиграл одну партию, а второй – ни одной, Паскаль приводит формулу  W=A+A*(1*3*5*...*(2n-1))/(2*4*6*...2n), где А – ставка каждого игрока, а W – ожидание выигрыша первого игрока.

Как видно, во всех случаях Паскаль делит ставку пропорционально вероятности выигрыша при продолжении игры. Оригинальный метод Паскаля трудно применить к более сложным случаям.

Задачи Пьеро Ферма. Пусть до выигрыша всей встречи игроку А недостает двух партий, а игроку В – трех. Как справедливо разделить ставку, если игра прервана?

Решение. Письмо Ферма , в котором он излагает свой метод решения, не сохранилось, но его можно восстановить из ответного письма Паскаля от 24 августа 1654 года. Рассуждение Ферма сводится к следующему. Игра может быть продолжена максимум еще 4 партии. Для перебора всех возможных случаев Ферма составляет таблицу, где выигрыши партий игроками А и В обозначены соответственно буквами а и в. Из 16 возможных исходов первые 11 благоприятны для выигрыша игроком А всей встречи, а остальные 5 исходов благоприятны для игрока В. следовательно, 11/16 ставки должен получить игрок А, а игрок В – 5/16. Как видно, Ферма предлагает разделить ставку пропорционально вероятностям выигрыша всей встречи.

    Паскаль решает эту задачу на основе изучения свойств арифметического треугольника, приведенного в его «Трактате об арифметическом треугольнике», опубликованном посмертно в Париже в 1665 году. Он складывает количество партий, недостающих игрокам А (2) и В (3) берет ту строку треугольника (рис. 1), в котором количество членов равно найденной сумме, то есть пятую.

1   1      1

1     2     1

1      3     3     1

1     4     6     4      1

Рис. 1.

  Тогда доля игрока А будет равна сумме  членов найденной строки, начиная от единицы, причем количество слагаемых равно числу партий, недостающих игроку В (3), а доля игрока В равна такой же сумме, но с количеством слагаемых, равном числу партий, недостающих игроку А (2). Выписываем строку, в котором находятся пять чисел. Это будет 1, 4, 6, 4, 1.  следовательно, ставку нужно разделить в отношении 11:5. при таком решении ставка делится пропорционально вероятностям выиграть всю ставку для игроков А и В.

То есть, правило Паскаля состоит в следующем : пусть игроку А до выигрыша всей игры не хватает m  партий , а игроку В – n партий, тогда ставка должна делиться между игроками в отношении .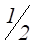

1.                                                                                                                                                                                                                                     

Пусть до выигрыша всей встречи игроку А недостает одного очка, а двум другим (В и С) недостает по два очка. Как справедливо разделить ставки?

Решение. Перебор всех возможных случаев можно представить таблицей.

При рассмотрении такой таблицы Паскаль допустил неточность в рассуждениях, считая, что из 27 возможных исходов бесспорно благоприятствуют игроку А лишь 13, а исходы пятого, одиннадцатого, девятнадцатого столбцов благоприятствуют сразу и игроку А и игроку В (аналогичные исходы девятого, пятнадцатого, двадцать четвертого столбцов благоприятствуют игроку А и игроку С). Поэтому доли игроков в этих случаях следует  брать с половинным весом. В результате Паскаль ошибочно предлагал делить ставку в отношении 16: 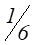 вместо 17:5:5.

Задачи о гаданиях.

По преданию, когда – то в сельских местностях России среди девушек существовало гадание. Одна из подруг зажимала в руке шесть травинок так, чтобы концы травинок торчали сверху и снизу, а другая связывала эти травинки попарно между собой сверху и снизу. Если при этом все шесть травинок оказывались связанными в одно кольцо, то это должно было означать, что девушка в текущем году выйдет замуж. 

Задача (для самостоятельного решения).

Какова вероятность того, что травинки при завязывании наудачу образуют кольцо?

Ответ. 8/15.